Equation Sheets
Equation Sheets

CHEM E 310 Material and Energy Balances

  
Contents
Description Equations
Units of force 1 N=1 kg⋅m/s21 lbf=32.174 lbm⋅ft/s2\begin{aligned}1 \ \mathrm{N} &= 1 \ \mathrm{kg \cdot m/s^2} \cr 1 \ \mathrm{lb_f} &= 32.174 \ \mathrm{lb_m \cdot ft/s^2}\end{aligned}
Weight W=mgW = mg
Gravitational acceleration g=9.8066 m/s2=32.174 ft/s2\begin{aligned}g &= 9.8066 \ \mathrm{m/s^2} \cr &= 32.174 \ \mathrm{ft/s^2}\end{aligned}
Description Equations
Mass flow rate m˙=dmdt\dot{m} = \dfrac{dm}{dt}
Volumetric flow rate V˙=dVdt\dot{V} = \dfrac{dV}{dt}
Molar flow rate n˙=dndt\dot{n} = \dfrac{dn}{dt}
Density ρ=mV=m˙V˙\rho = \dfrac{m}{V} = \dfrac{\dot{m}}{\dot{V}}
Specific volume v=Vm=1ρv = \dfrac{V}{m} = \dfrac{1}{\rho}
Molar volume Vm=Vn=MρV_{\mathrm{m}} = \dfrac{V}{n} = \dfrac{M}{\rho}
Specific gravity SG=ρρref\mathrm{SG} = \dfrac{\rho}{\rho_{\mathrm{ref}}}
Description Equations
Mole and molecular wieght n=mMn = \dfrac{m}{M}
Mass fraction xA=mAmx_A = \dfrac{m_A}{m}
Mole fraction yA=nAny_A = \dfrac{n_A}{n}
Scaling factor of percent (%),
parts per million (ppm),
parts per billion (ppb)		 ×100%×106 ppm×109 ppb\times 100\% \newline \times 10^6 \ \mathrm{ppm} \newline \times 10^9 \ \mathrm{ppb}
Average molecular weight M‾=∑mi∑ni=∑yiMi=(∑x1Mi)−1\overline{M} = \dfrac{\sum m_i}{\sum n_i} = \sum y_i M_i = \left(\sum\dfrac{x_1}{M_i}\right)^{-1}
Mass concentration ρA=mAV\rho_A = \dfrac{m_A}{V}
Molar concentration cA=nAVc_A = \dfrac{n_A}{V}
Molarity and molar 1 M=1 mol/L1 \ \mathrm{M} = 1 \ \mathrm{mol}/\mathrm{L}
Description Equations
Pressure P=FAP = \dfrac{F}{A}
Hydrostatic pressure P=P0+ρghP = P_0 + \rho gh
Hydrostatic head P=ρgPhP = \rho gP_h
Relationship between pressures Pabs=Patm+PgaugeP_{\text{abs}} = P_{\text{atm}} + P_{\text{gauge}}
General manometer P1+ρ1gd1=P2+ρ2gda+ρmghP_1 + \rho_1 g d_1 = P_2 + \rho_2 g d_a + \rho_m g h
Differential manometer P1−P2=(ρm−ρ)ghP_1 - P_2 = (\rho_m - \rho)gh
Manometer for gas P1−P2=ρmgh=PhP_1 - P_2 = \rho_m gh = P_h
SCFM (standard cubic feet per minute) and ACFM (actual cubic feet per minute) Va˙=Vs˙PsPaTaTs (ideal gas)\dot{V_{\text{a}}} = \dot{V_{\text{s}}}\dfrac{P_{\text{s}}}{P_{\text{a}}} \dfrac{T_{\text{a}}}{T_{\text{s}}} \ (\text{ideal gas})
Standard condition of gases natural gas - 59∘F,1 atm59 ^\circ\mathrm{F}, 1 \ \mathrm{atm}
other gas - 0∘C,1 atm0 ^\circ\mathrm{C}, 1 \ \mathrm{atm}
Description Equations
Conversion of temperature T(K)=T(∘C)+273.15T(∘R)=T(∘F)+459.67T(∘R)=1.8T(K)T(∘F)=1.8T(∘C)+32T(\mathrm{K}) = T(\mathrm{^\circ C}) + 273.15 \newline T(\mathrm{^\circ R}) = T(\mathrm{^\circ F}) + 459.67 \newline T(\mathrm{^\circ R}) = 1.8 T(\mathrm{K}) \newline T(\mathrm{^\circ F}) = 1.8 T(\mathrm{^\circ C}) + 32
Conversion of temperature intervals 1∘C=1.8∘F1∘R=1.8 K1∘F=1∘R1∘C=1.8 K1 ^\circ\mathrm{C} = 1.8 ^\circ\mathrm{F} \newline 1 ^\circ\mathrm{R} = 1.8 \ \mathrm{K} \newline 1 ^\circ\mathrm{F} = 1 ^\circ\mathrm{R} \newline 1 ^\circ\mathrm{C} = 1.8 \ \mathrm{K}
Description Equations
Balance equation Accumulation = Input - Output
+ Generation - Consumption
Fractional excess Fractional excess=nfed−nstoichnstoich\text{Fractional excess} = \dfrac{n_{\mathrm{fed}} - n_{\mathrm{stoich}}}{n_{\mathrm{stoich}}}
Fractional conversion Fractional conversion=nreactednfed\text{Fractional conversion} = \dfrac{n_{\mathrm{reacted}}}{n_{\mathrm{fed}}}
Fractional completion of limiting reactant Fractional completion=nreactednfed=−νξnfed\text{Fractional completion} = \dfrac{n_{\mathrm{reacted}}}{n_{\mathrm{fed}}} = \dfrac{-\nu\xi}{n_{\mathrm{fed}}}
Extent of reaction ξ=ni−ni0νi\xi = \dfrac{n_i - n_{i0}}{\nu_i}
Extent of reaction in multiple reactions ni=ni0∑jνijξijn_i = n_{i0}\sum\limits_j\nu_{ij}\xi_{ij}
Yield
theoretical = complete rxn, no side rxn		 Yield=nactualntheoretical×100\text{Yield} = \dfrac{n_\text{actual}}{n_\text{theoretical}} \times 100%
Selectivity Selectivity=ndesirednundesired\text{Selectivity} = \dfrac{n_\text{desired}}{n_\text{undesired}}
Fractional excess of air (oxygen) Fractional excess air=nfed−nstoichnstoich\text{Fractional excess air} = \dfrac{n_{\mathrm{fed}} - n_{\mathrm{stoich}}}{n_{\mathrm{stoich}}}
Quality of steam Quality of steam=mvapormtotal\text{Quality of steam} = \dfrac{m_{\text{vapor}}}{m_{\text{total}}}
Description Equations
Nonreactive process No. unknown variables−No. independent material balance species−No. other relations (process specifications)No. degrees of freedom\small\begin{aligned} & \text{No. unknown variables} \cr - & \text{No. independent material balance species} \cr - & \text{No. other relations (process specifications)} \cr \hline & \text{No. degrees of freedom}\end{aligned}
Reactive process
Molecular species balance method
1 reaction system		 No. unknown variables+No. independent reaction−No. independent molecular species−No. other relationsNo. degrees of freedom\small\begin{aligned} & \text{No. unknown variables} \cr + & \text{No. independent reaction} \cr - & \text{No. independent molecular species} \cr - & \text{No. other relations} \cr \hline & \text{No. degrees of freedom}\end{aligned}
Reactive process
Atomic species balance method
>1 reaction system		 No. unknown variables−No. independent reactive atomic species−No. independent nonreactive molecular species−No. other relationsNo. degrees of freedom\small\begin{aligned} & \text{No. unknown variables} \cr - & \text{No. independent reactive atomic species} \cr - & \text{No. independent nonreactive molecular species} \cr - & \text{No. other relations} \cr \hline & \text{No. degrees of freedom}\end{aligned}
Reactive process
Extent of reaction method
equilibrium problem		 No. unknown variables+No. independent reaction−No. independent reactive species−No. independent nonreactive species−No. other relationsNo. degrees of freedom\small\begin{aligned} & \text{No. unknown variables} \cr + & \text{No. independent reaction} \cr - & \text{No. independent reactive species} \cr - & \text{No. independent nonreactive species} \cr - & \text{No. other relations} \cr \hline & \text{No. degrees of freedom}\end{aligned}
Description Equations
Estimations of density of liquid mixtures
1. Experimental data
2. Estimation formula
★ Volume addativity		 1ρˉ=∑i=1nxiρiρˉ=∑i=1nxiρ1\dfrac{1}{\bar{\rho}} = \sum\limits_{i=1}^n \dfrac{x_i}{\rho_i} \newline \bar{\rho} = \sum\limits_{i=1}^n x_i\rho_1
Incompressible approximation ∂V^=0(∂V^∂P)T=0(∂V^∂T)P=0\partial\hat{V} = 0 \newline \left(\frac{\partial\hat{V}}{\partial P}\right)_T = 0 \newline \left(\frac{\partial\hat{V}}{\partial T}\right)_P = 0
Volume expansivity β=1V^(∂V^∂T)P\beta = \dfrac{1}{\hat{V}} \left(\dfrac{\partial\hat{V}}{\partial T}\right)_P
Isothermal compressibility K=−1V^(∂V^∂P)TK = -\dfrac{1}{\hat{V}} \left(\dfrac{\partial\hat{V}}{\partial P}\right)_T
Volume with change in T,PT, P ln⁡(V^2V^1)=β(T2−T1)−K(P2−P1)\ln\left(\dfrac{\hat{V}_2}{\hat{V}_1}\right) = \beta(T_2 - T_1) - K(P_2 - P_1)
Description Equations
Specific molar volume V^=Vn\hat{V} = \dfrac{V}{n}
Ideal gas equation of state
★ T>0∘C,P<1 atm\footnotesize T > 0\mathrm{^\circ C}, P < 1 \ \mathrm{atm}		 PV=nRTPV^=RTPV = nRT \newline P\hat{V} = RT
Standard conditions and actual conditions PVPsVs^=nTTs\dfrac{PV}{P_{\text{s}}\hat{V_{\text{s}}}} = n\dfrac{T}{T_{\text{s}}}
SCFM vs. ACFM
★ Ideal gas		 Va˙=Vs˙PsPaTaTs\dot{V_{\text{a}}} = \dot{V_{\text{s}}}\dfrac{P_{\text{s}}}{P_{\text{a}}} \dfrac{T_{\text{a}}}{T_{\text{s}}}
Ideal gas condition T>0∘CP<1 atmV^ideal=RTP{>5 L/mol,80 ft3/lbmoldiatomic>20 L/mol,320 ft3/lbmolotherT > 0 \mathrm{^\circ C} \newline P < 1 \ \mathrm{atm} \newline \footnotesize\hat{V}_{\text{ideal}} = \dfrac{RT}{P} \newline \begin{cases} >5 \ \mathrm{L/mol}, 80 \ \mathrm{ft^3/lbmol} & \text{diatomic} \cr >20 \ \mathrm{L/mol}, 320 \ \mathrm{ft^3/lbmol} & \text{other} \end{cases}
Description Equations
Partial pressure Pi=yiPP_i = y_i P
Dalton’s law ∑Pi=P\sum P_i = P
Pure-component volume Vi=yiVV_i = y_i V
Amagat’s law ∑Vi=V\sum V_i = V
Volume fraction of ideal gas yi=ViVy_i = \dfrac{V_i}{V}
Description Equations
van der Waals equation of state P=RTV^−b−aV^2P = \dfrac{RT}{\hat{V} - b} - \dfrac{a}{\hat{V}^2}
Constant a=27R2Tc264Pca = \dfrac{27R^2T_c^2}{64P_c}
Constant b=RTc8Pcb = \dfrac{RT_c}{8P_c}
Significance of 3 real roots V^highest=V^sat, vaporV^lowest=V^sat, liquidV^middle=no significance\hat{V}_{\text{highest}} = \hat{V}_{\text{sat, vapor}} \newline \hat{V}_{\text{lowest}} = \hat{V}_{\text{sat, liquid}} \newline \hat{V}_{\text{middle}} = \small \text{no significance}
Significance of real and imaginary roots V^real=V^gasV^imaginary=no significance\hat{V}_{\text{real}} = \hat{V}_{\text{gas}} \newline \hat{V}_{\text{imaginary}} = \small\text{no significance}
Description Equations
Virial equation of state PV^RT=1+BV^+CV^2+DV^3+⋯\dfrac{P\hat{V}}{RT} = 1 + \dfrac{B}{\hat{V}} + \dfrac{C}{\hat{V}^2} + \dfrac{D}{\hat{V}^3} + \cdots
First order appox. of virial equation of state PV^RT=1+BPRT\dfrac{P\hat{V}}{RT} = 1 + \dfrac{BP}{RT}
Reduced temperature Tr=TTcT_r = \dfrac{T}{T_c}
Reduced pressure Pr=PPcP_r = \dfrac{P}{P_c}
  1. Lookup Tc,Pc,ωT_c, P_c, \omega
  2. Calculate TrT_r
  3. Estimate B by
    1. B0=0.083−0.422Tr1.6B_0 = 0.083 - \dfrac{0.422}{T_r^{1.6}}
    2. B1=0.139−0.172Tr4.2B_1 = 0.139 - \dfrac{0.172}{T_r^{4.2}}
    3. B=RTcPc(B0+ωB1)B = \dfrac{RT_c}{P_c}(B_0 + \omega B_1)
  4. Substitute known values into first order approximation
Description Equations
SRK equation of state P=RTV^−b−aT0.5V^(V^+b)P = \dfrac{RT}{\hat{V} - b} - \dfrac{a}{T^{0.5}\hat{V}(\hat{V}+b)}
Constants a=0.4274R2Tc2.5/Pcb=0.08664RTc/Pca = 0.4274 R^2 T_c^{2.5} / P_c \newline b = 0.08664 RT_c / P_c
Description Equations
SRK equation of state P=RTV^−b−αaV^(V^+b)P = \dfrac{RT}{\hat{V} - b} - \dfrac{\alpha a}{\hat{V}(\hat{V}+b)}
Constants a=0.4274(RTc)2/Pcb=0.08664RTc/Pcm=0.48508+1.55171ω−0.1561ω2Tr=T/Tcα=[1+m(1−Tr)]2a = 0.4274 (RT_c)^2 / P_c \newline b = 0.08664 RT_c / P_c \newline m = 0.48508 + 1.55171\omega - 0.1561\omega^2 \newline T_r = T/T_c \newline \alpha = [1 + m(1-\sqrt{T_r})]^2
  1. Lookup Tc,Pc,ωT_c, P_c, \omega
  2. Calculate a,b,ma, b, m
  3. Determine the known
    1. If known T,V^T, \hat{V}
      1. Calculate Tr,αT_r, \alpha
      2. Solve from equation directly for PP
    2. If known T,PT, P
      1. Use equation and all knowns
      2. Use python to solve for V^\hat{V}
    3. If known P,V^P, \hat{V}
      1. Use equation, Tr,αT_r, \alpha, and all knowns
      2. Use python to solve for TT
Description Equations
Compressibility
(Law of corresponding state)		 z=PV^RTz = \dfrac{P\hat{V}}{RT}
Compressibility-factor equation of state PV^=zRTP\hat{V} = zRT
Reduced temperature Tr=TTcT_r = \dfrac{T}{T_c}
Reduced pressure Pr=PPcP_r = \dfrac{P}{P_c}
Ideal reduced volume V^rideal=PcV^RTc\hat{V}_r^{\text{ideal}} = \dfrac{P_c\hat{V}}{RT_c}
Kay’s rule of nonideal gas mixtures
Pseudocritical temperature		 Tc′=∑yiTciT_c' = \sum y_i T_{ci}
Pseudocritical pressure Pc′=∑yiPciP_c' = \sum y_i P_{ci}
Pseudoreduced temperature Tr′=TTc′T_r' = \dfrac{T}{T_c'}
Pseudoreduced pressure Pr′=PPc′P_r' = \dfrac{P}{P_c'}
Ideal pseudoreduced volume V^rideal=Pc′V^RTc′\hat{V}_r^{\text{ideal}} = \dfrac{P_c'\hat{V}}{RT_c'}
  1. Lookup Tc,PcT_c, P_c
  2. If gas is HX2/He\ce{H2/He}, adjust critical constant by Newton’s correlation
    1. Tca=Tc+8 KT_c^a = T_c + 8 \ \mathrm{K}
    2. Pca=Pc+8 atmP_c^a = P_c + 8 \ \mathrm{atm}
  3. Calculate reduced value of two known variables from Tr,Pr,VridealT_r, P_r, V_r^{\text{ideal}}
  4. Use compressibility chart to determine zz
  5. Solve for unknowns from equation
Description Equations
Clapeyron equation dP∗dt=ΔH^vT1Vg^−Vl^\dfrac{dP^*}{dt} = \dfrac{\Delta \hat{H}_\text{v}}{T}\dfrac{1}{\hat{V_g} - \hat{V_l}}
Clapeyron equation d(ln⁡P∗)d(1/T)=−ΔH^vR\dfrac{d(\ln P^*)}{d(1/T)} = -\dfrac{\Delta \hat{H}_\text{v}}{R}
Clausius-Clapeyron equation ln⁡P∗=−ΔH^vRT+B\ln P^* = -\dfrac{\Delta \hat{H}_\text{v}}{RT} + B
Clausius-Clapeyron equation ln⁡(P2P1)=−ΔH^vnR(1T2−1T1)\ln \left(\dfrac{P_2}{P_1}\right) = -\dfrac{\Delta \hat{H}_\text{v}}{nR} \left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)
Antoine equation
(Vapor pressure of species)		 log⁡10P∗=A−BT+C\log_{10}P^* = A - \dfrac{B}{T+C}
Description Equations
Gibbs phase rule F=2+c−Π−r\mathcal{F} = 2 + c - \Pi - r
Total vapor pressure of immiscible liquids P=∑Pi∗P = \sum P_i^*
Raoult’s law
★ Ideal gas and solution, non-dilute xAx_A		 PA=yAP=xAPA∗(T)P_A = y_AP = x_AP_A^*(T)
Henry’s law
★ Ideal gas and solution, dilute xAx_A		 PA=yAP=xAHA(T)P_A = y_AP = x_AH_A(T)
VLE of real gases
φ\varphi - fugacity coefficient
γ\gamma - activity coefficient		 yiφiP=xiγiP∗y_i\varphi_i P = x_i\gamma_i P^*
Partition coefficient of ideal gas (Raoult’s law)
★ Ideal gas: φ=1,γ=1\footnotesize\varphi = 1, \gamma = 1		 Ki=yixi=γiPi∗φiP=Pi∗PK_i = \dfrac{y_i}{x_i} = \dfrac{\gamma_i P_{i}^{*}}{\varphi_i P} = \dfrac{P_{i}^{*}}{P}
Partition coefficient of ideal gas (Henry’s law)
★ Ideal gas, Henry’s law assumptions		 Ki=HiPK_i = \dfrac{H_i}{P}
Description Equations
Relative saturation/humidity sr=PAPA∗(T)×100s_r = \dfrac{P_A}{P_A^*(T)}\times 100%
Molal saturation/humidity sm=PAP−PAs_m = \dfrac{P_A}{P-P_A}
Absolute saturation/humidity sa=PAMA(P−PA)MAs_a = \dfrac{P_AM_A}{(P-P_A)M_A}
Percent saturation/humidity sp=smsm∗×100%=PA/(P−PA)PA∗/(P−PA∗)×100%s_p = \dfrac{s_m}{s_m^*}\times 100 \% \newline = \dfrac{P_A/(P-P_A)}{P_A^*/(P-P_A^*)}\times 100 \%
Description Equations
Superheated vapor PA=yAP<PA∗(T)P_A = y_AP < P_A^*(T)
Saturated vapor and dew point PA=yAP=PA∗(Tdp)P_A = y_AP = P_A^*(T_{\text{dp}})
Degree of superheat T−TdpT - T_{\text{dp}}
Bubble point temperature of mixture at constant PP P=∑xiPi∗(Tbp)P = \sum x_iP_i^*(T_{\text{bp}})
Bubble point pressure of mixture at constant TT Pbp=∑xiPi∗(T)P_{\text{bp}} = \sum x_iP_i^*(T)
Dew point temperature of mixture at constant PP ∑yiPi∗(Tdp)=1\sum\dfrac{y_i}{P_i^*(T_{\text{dp}})}= 1
Dew point pressure of mixture at constant TT Pdp=[∑yiPi∗(T)]−1P_{\text{dp}} = \left[ \sum\dfrac{y_i}{P_i^*(T)} \right]^{-1}
Description Equations
Kinetic energy Ek=12mv2E_k = \frac{1}{2}mv^2
Potential energy Ep=mgzE_p = mgz
Internal energy U(T,V)U(T, V)
Total energy E=U+Ek+EpE = U + E_k + E_p
Work W=PΔVW = P\Delta V
Closed system balance ΔU+ΔEk+ΔEp=Q+W\Delta U + \Delta E_k + \Delta E_p = Q+W
ΔEk=0\Delta E_k = 0 Not accelerating
ΔEp=0\Delta E_p = 0 Not changing height
ΔU=0\Delta U = 0 No phase change, chemical reaction, temperature change
Q=0Q = 0 Insulated system; adiabatic; temperature of system and surrounding the same
W=0W = 0 No moving parts, radiation, electric current, flow
Description Equations
Work W˙=W˙s+W˙fl\dot{W} = \dot{W}_s + \dot{W}_{fl}
Enthalpy H=U+PVH = U+PV
Specific properties V^=Vm,V^=Vn\hat{V} = \frac{V}{m}, \hat{V} = \frac{V}{n}
Open system balance ΔH˙+ΔE˙k+ΔE˙p=Q˙+W˙s\Delta \dot{H} + \Delta \dot{E}_k + \Delta \dot{E}_p = \dot{Q} + \dot{W}_s
ΔEk=0\Delta E_k = 0 No acceleration; linear velocity of all streams the same
ΔEp=0\Delta E_p = 0 Stream entering and leaving at same height
Q˙=0\dot{Q} = 0 Insulated; adiabatic; system and surrounding temperature the same
W˙s=0\dot{W}_s = 0 No moving parts
Friction loss F^=ΔU^−Q˙m˙\hat{F} = \Delta\hat{U} - \dfrac{\dot{Q}}{\dot{m}}
Mechanical energy balance ΔPρ+Δv22+gΔz+F^=W˙sm˙\dfrac{\Delta P}{\rho} + \dfrac{\Delta v^2}{2} + g\Delta z + \hat{F} = \dfrac{\dot{W}_s}{\dot{m}}
Bernoulli equation
★ F^=0,W˙s=0\footnotesize \hat{F}=0, \dot{W}_s=0		 ΔPρ+Δv22+gΔz=0\dfrac{\Delta P}{\rho} + \dfrac{\Delta v^2}{2} + g\Delta z = 0
Description Equations
Internal energy ΔU={=0(ideal gas)≈0(real gas) P<10 bar≠0(real gas) P>10 bar≈0(condensed phases)\Delta U = \begin{cases} = 0 & \text{(ideal gas)} \cr \approx 0 & \text{(real gas) }P<10 \ \mathrm{bar} \cr \not= 0 & \text{(real gas) }P>10 \ \mathrm{bar} \cr \approx 0 & \text{(condensed phases)} \end{cases}
Enthalpy ΔH={=0(ideal gas)≈0(real gas) P<10 bar≠0(real gas) P>10 bar≈V^ΔP(condensed phases)\Delta H = \begin{cases} = 0 & \text{(ideal gas)} \cr \approx 0 & \text{(real gas) }P<10 \ \mathrm{bar} \cr \not= 0 & \text{(real gas) }P>10 \ \mathrm{bar} \cr \approx \hat{V}\Delta P & \text{(condensed phases)} \end{cases}

Use (hypothetical) process paths to guide the use of equations.

Description Equations
Heat capacity at constant volume CV(T)=(∂U^∂T)VC_V(T) = \left(\frac{\partial\hat{U}}{\partial T}\right)_V
Heat capacity at constant pressure CP(T)=(∂H^∂T)PC_P(T) = \left(\frac{\partial\hat{H}}{\partial T}\right)_P
Heat capacity correlation CP(T)=a+bT+cT2+dT3C_P(T) = a+bT+cT^2+dT^3
Heat capacity relation of condensed phases CP≈CVC_P \approx C_V
Heat capacity relation of ideal gas CP=CV+RC_P = C_V+R
Heat capacity of monoatmoic ideal gases CV=32R,CP=52RC_V = \frac{3}{2}R, C_P = \frac{5}{2}R
Heat capacity of polyatomic ideal gases CV=52R,CP=72RC_V = \frac{5}{2}R, C_P = \frac{7}{2}R
Kopp’s rule
Heat capacity of compound (table B.10)		 CP,compound=∑νiCP,iC_{P, \text{compound}} = \sum \nu_i C_{P, i}
Kopp’s rule
Heat capacity of mixture		 CP,mix=∑yiCP,i(T)C_{P, \text{mix}} = \sum y_i C_{P, i}(T)
Change in internal energy at changing temperature ΔU^=∫T1T2CV(T) dT\Delta\hat{U} = \int_{T_1}^{T_2}C_V(T) \ dT
Change in enthalpy at changing temperature ΔH^=∫T1T2CP(T) dT\Delta\hat{H} = \int_{T_1}^{T_2}C_P(T) \ dT
Description Equations
Latent heat approximation of condensed phases ΔU≈ΔH\Delta U \approx \Delta H
Latent heat approximation of ideal gas ΔUv≈ΔHv−RT\Delta U_{\text{v}} \approx \Delta H_{\text{v}} - RT
Description Equations
Heat of reaction of batch process ΔH=ξΔHrxn(T1,P1)\Delta H = \xi \Delta H_{\text{rxn}}(T_1, P_1)
Heat of reaction of continuous process ΔH˙=ξΔH˙rxn(T1,P1)\Delta \dot{H} = \xi \Delta \dot{H}_{\text{rxn}}(T_1, P_1)
Endothermic reaction ΔHrxn>0\Delta H_{\text{rxn}} > 0
Exothermic reaction ΔHrxn<0\Delta H_{\text{rxn}} < 0
Hess’s law and heat of formation
“product minus reactant”		 ΔHrxn∘=∑iνiΔH^f,i∘\Delta H_{\text{rxn}}^\circ = \sum\limits_i \nu_i \Delta \hat{H}_{\text{f}, i}^\circ
Heat of formation conventions ΔH^f∘(elemental)=0\Delta \hat{H}_{\text{f}}^\circ(\text{elemental}) = 0
Hess’s law and heat of combustion
“reactant minus product”		 ΔHrxn∘=−∑iνiΔH^c,i∘\Delta H_{\text{rxn}}^\circ = -\sum\limits_i \nu_i \Delta \hat{H}_{\text{c}, i}^\circ
Heat of combustion conventions ΔH^c∘(O2)=0ΔH^c∘(combustion product)=0\Delta \hat{H}_{\text{c}}^\circ(\mathrm{O_2}) = 0 \newline \Delta \hat{H}_{\text{c}}^\circ(\text{combustion product}) = 0
combustion product: COX2,HX2O,SOX2,NX2\small\ce{CO2, H2O, SO2, N2}
Internal energy of reaction
(product ν>0\nu>0; reactant ν<0\nu<0)		 ΔUrxn=ΔHrxn−RT∑gasνi\Delta U_{\text{rxn}} = \Delta H_{\text{rxn}} - RT \sum\limits_{\text{gas}}\nu_i
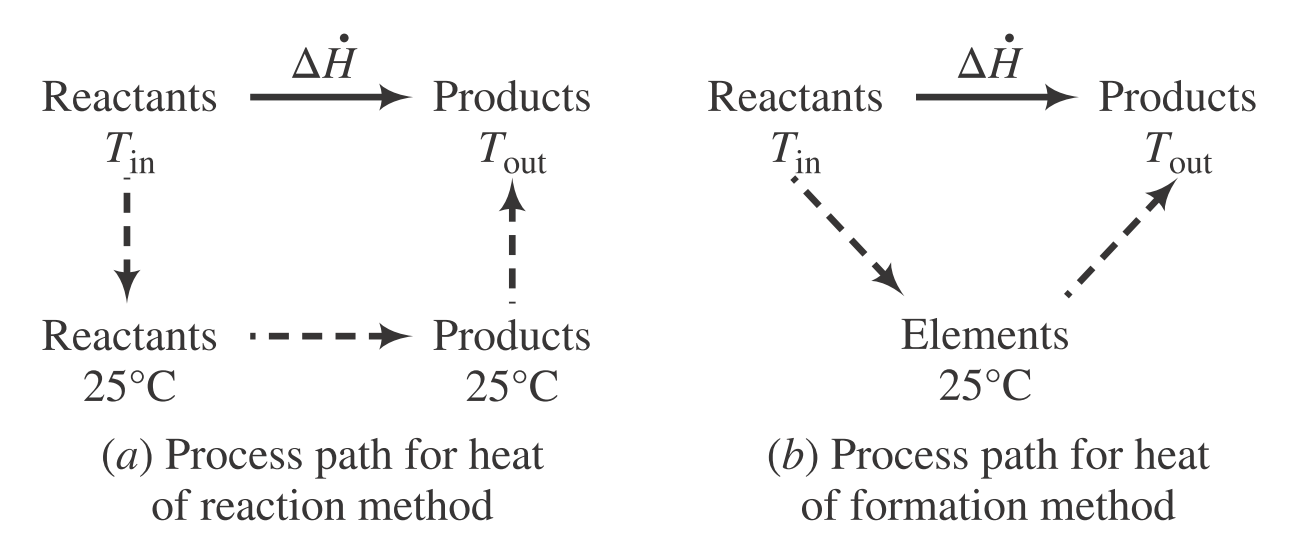
/cheme/cheme-310-reaction-process-path.png
Reaction process paths. (Elementary Principles of Chemical Processes 4e by Felder et al. p507.)
Description Equations
Enthalpy change of heat of reaction method ΔH˙=∑rxnξΔHrxn∘+∑n˙outH^out−∑n˙inH^in\Delta \dot{H} = \sum\limits_{\text{rxn}} \xi \Delta H_{\text{rxn}}^\circ + \sum \dot{n}_{\text{out}}\hat{H}_{\text{out}} - \sum \dot{n}_{\text{in}}\hat{H}_{\text{in}}
Enthalpy change of heat of formation method ΔH˙=∑n˙outH^out−∑n˙inH^in\Delta \dot{H} = \sum \dot{n}_{\text{out}}\hat{H}_{\text{out}} - \sum \dot{n}_{\text{in}}\hat{H}_{\text{in}}
Updated on 2021-08-17
Back | Home