Equation Sheets
Equation Sheets

Contents

CHEM E 326 Chemical Engineering Thermodynamics

  
Contents
Description Equations
Mechanical equilibrium Psys=PsurrP_{\text{sys}} = P_{\text{surr}}
Thermal equilibrium Tsys=TsurrT_{\text{sys}} = T_{\text{surr}}
Chemical equilibrium μ(t1)=μ(t2)\mu(t_1) = \mu(t_2)
Gibbs phase rule F=2+c−p−r\mathcal{F} = 2 + c - p - r
Quality x=nvnl+nv=v−vlvv−vlx = \dfrac{n_v}{n_l + n_v} = \dfrac{v - v_l}{v_v - v_l}
Critical point (∂P∂v)Tc=0,(∂2P∂v2)Tc=0\left( \dfrac{\partial P}{\partial v} \right)_{T_c} = 0, \left( \dfrac{\partial^2 P}{\partial v^2} \right)_{T_c} = 0
System Type Equations
Closed systems Δu+ΔeK+ΔeP=q+w\Delta u + \Delta e_K + \Delta e_P = q + w
Closed systems Δu=q+w\Delta u = q + w
Open systems dUdt=∑inn˙ihi+∑outn˙ihi+Q˙+W˙s\dfrac{dU}{dt} = \sum\limits_{\text{in}}\dot{n}_i h_i + \sum\limits_{\text{out}}\dot{n}_i h_i + \dot{Q} + \dot{W}_s
Open system at steady state 0=∑inn˙ihi+∑outn˙ihi+Q˙+W˙s0 = \sum\limits_{\text{in}}\dot{n}_i h_i + \sum\limits_{\text{out}}\dot{n}_i h_i + \dot{Q} + \dot{W}_s
Description Equations
Work w=−∫Pextdvw = - \int P_{\text{ext}} dv
Enthalpy h=u+Pvh = u + Pv
Efficiency of irreversible isothermal expansion η=wirrevwrev\eta = \dfrac{w_{\text{irrev}}}{w_{\text{rev}}}
Efficiency of irreversible isothermal compression η=wrevwirrev\eta = \dfrac{w_{\text{rev}}}{w_{\text{irrev}}}
Description Equations
Constant volume heat capacity cv=(∂u∂T)vc_v = \left(\dfrac{\partial u}{\partial T}\right)_v
Constant pressure heat capacity cP=(∂h∂T)Pc_P = \left(\dfrac{\partial h}{\partial T}\right)_P
Ideal gas heat capacity cP=cv+Rc_P = c_v + R
Condensed phase heat capacity (l, s) cP≈cvc_P \approx c_v
Mean heat capacity of gas cˉP=1T2−T1∫T1T2cP(T)dT\bar{c}_P = \dfrac{1}{T_2 - T_1} \displaystyle\int_{T_1}^{T_2} c_P(T) dT
Description Equations
Enthalpy of vaporization Δhvap=hv−hl\Delta h_{\text{vap}} = h_v - h_l
Enthalpy of fusion Δhfus=hs−hl\Delta h_{\text{fus}} = h_s - h_l
Enthalpy of sublimation Δhsub=hv−hs\Delta h_{\text{sub}} = h_v - h_s
Enthalpy of phase change at any TT Δhvap(T)=Δhvap(Tb)+∫TbT(cPv−cPl)dT\Delta h_{\text{vap}}(T) = \Delta h_{\text{vap}}(T_b) + \int_{T_b}^{T} (c_P^{v} - c_P^l)dT
Enthalpy of reaction Δhrxn∘=∑νiΔhf,i\Delta h_{\text{rxn}}^\circ = \sum \nu_i \Delta h_{f, i}
System Type Equations
Isolated system ΔSuniv≥0\Delta S_{\text{univ}} \ge 0
Closed system ΔSsys−QsysTsurr≥0\Delta S_{\text{sys}} - \dfrac{Q_{\text{sys}}}{T_{\text{surr}}} \ge 0
Open system ∑outn˙isi−∑inn˙isi−Q˙Tsurr+dSdt≥0\sum\limits_{\text{out}} \dot{n}_i s_i - \sum\limits_{\text{in}} \dot{n}_i s_i - \dfrac{\dot{Q}}{T_{\text{surr}}} + \dfrac{dS}{dt} \ge 0
Open system at steady state ∑outn˙isi−∑inn˙isi−Q˙Tsurr≥0\sum\limits_{\text{out}} \dot{n}_i s_i - \sum\limits_{\text{in}} \dot{n}_i s_i - \dfrac{\dot{Q}}{T_{\text{surr}}} \ge 0
Description Equations
Entropy ds=δqrevTds = \dfrac{\delta q_{\text{rev}}}{T}
Description γ\gamma Equation
Polytropic - PVγ=constPV^\gamma = \text{const}
Isobaric 00 P=constP = \text{const}
Isothermal 11 PV=constPV = \text{const}
Isentropic k=cPcvk = \dfrac{c_P}{c_v} PVk=constPV^k = \text{const}
Isochoric ∞\infty V=constV = \text{const}

Isoenergetic process (Δu=0  ⟹  ΔT=0\Delta u = 0 \implies \Delta T = 0) of ideal gas has similar analysis.

Description Equations
Condition
★ Ideal gas		 ΔT=0\Delta T = 0
Internal energy change Δu=0\Delta u = 0
Enthalpy change Δh=0\Delta h = 0
First law Δu=q+w=0\Delta u = q + w = 0
Work (changing volume) w=−∫RTvdv=−RTln⁡(v2v1)w = -\displaystyle\int \dfrac{RT}{v} dv = -RT\ln\left(\dfrac{v_2}{v_1}\right)
Work (changing pressure) w=∫RTPdP=RTln⁡(P2P1)w = \displaystyle\int \dfrac{RT}{P} dP = RT\ln\left(\dfrac{P_2}{P_1}\right)
Heat q=−wq = -w
Entropy change Δs=∫δqT=qT=−wT\Delta s = \displaystyle\int \dfrac{\delta q}{T} = \dfrac{q}{T} = -\dfrac{w}{T}
Entropy change (changing volume) Δs=Rln⁡(v2v1)\Delta s = R\ln\left(\dfrac{v_2}{v_1}\right)
Entropy change (changing concentration) Δs=−Rln⁡(c2c1)\Delta s = -R\ln\left(\dfrac{c_2}{c_1}\right)
Entropy change (changing pressure) Δs=−Rln⁡(P2P1)\Delta s = -R\ln\left(\dfrac{P_2}{P_1}\right)
Description Equations
Condition
★ Ideal gas		 q=0q = 0
First law Δu=w\Delta u = w
Enthalpy change Δh=Δu+RΔT\Delta h = \Delta u + R \Delta T
Work (changing volume) w=−∫RTvdv=−RTln⁡(v2v1)w = -\displaystyle\int \dfrac{RT}{v} dv = -RT\ln\left(\dfrac{v_2}{v_1}\right)
Work (changing pressure) w=∫RTPdP=RTln⁡(P2P1)w = \displaystyle\int \dfrac{RT}{P} dP = RT\ln\left(\dfrac{P_2}{P_1}\right)
Entropy change Δs=0\Delta s = 0
Heat capacity ratio γ=cPcv\gamma = \dfrac{c_P}{c_v}
PVT relationship P1V1γ=P2V2γT1V1γ−1=T2V2γ−1P1(1/γ)−1T1=P2(1/γ)−1T2P_1 V_1^\gamma = P_2 V_2^\gamma \newline T_1 V_1^{\gamma-1} = T_2 V_2^{\gamma-1} \newline P_1^{(1/\gamma)-1} T_1 = P_2^{(1/\gamma)-1} T_2
Description Equations
Condition
★ Ideal gas		 Δv=0\Delta v = 0
Work w=0w = 0
Internal energy change Δu=∫cv dT\Delta u = \displaystyle\int c_v \ dT
First law q=Δuq = \Delta u
Entropy change Δs=∫δqT=∫duT=∫cvT dT\Delta s = \displaystyle\int \dfrac{\delta q}{T} = \int \dfrac{du}{T} = \int \dfrac{c_v}{T} \ dT
Description Equations
Condition
★ Ideal gas		 ΔP=0\Delta P = 0
Internal energy change Δu=∫cv dT\Delta u = \displaystyle\int c_v \ dT
Enthalpy change Δh=∫cp dT\Delta h = \displaystyle\int c_p \ dT
Work w=−PΔvw = -P\Delta v
Heat q=Δhq = \Delta h
Entropy change Δs=∫δqT=∫dhT=∫cpT dT\Delta s = \displaystyle\int \dfrac{\delta q}{T} = \int \dfrac{dh}{T} = \int \dfrac{c_p}{T} \ dT
Description Equations
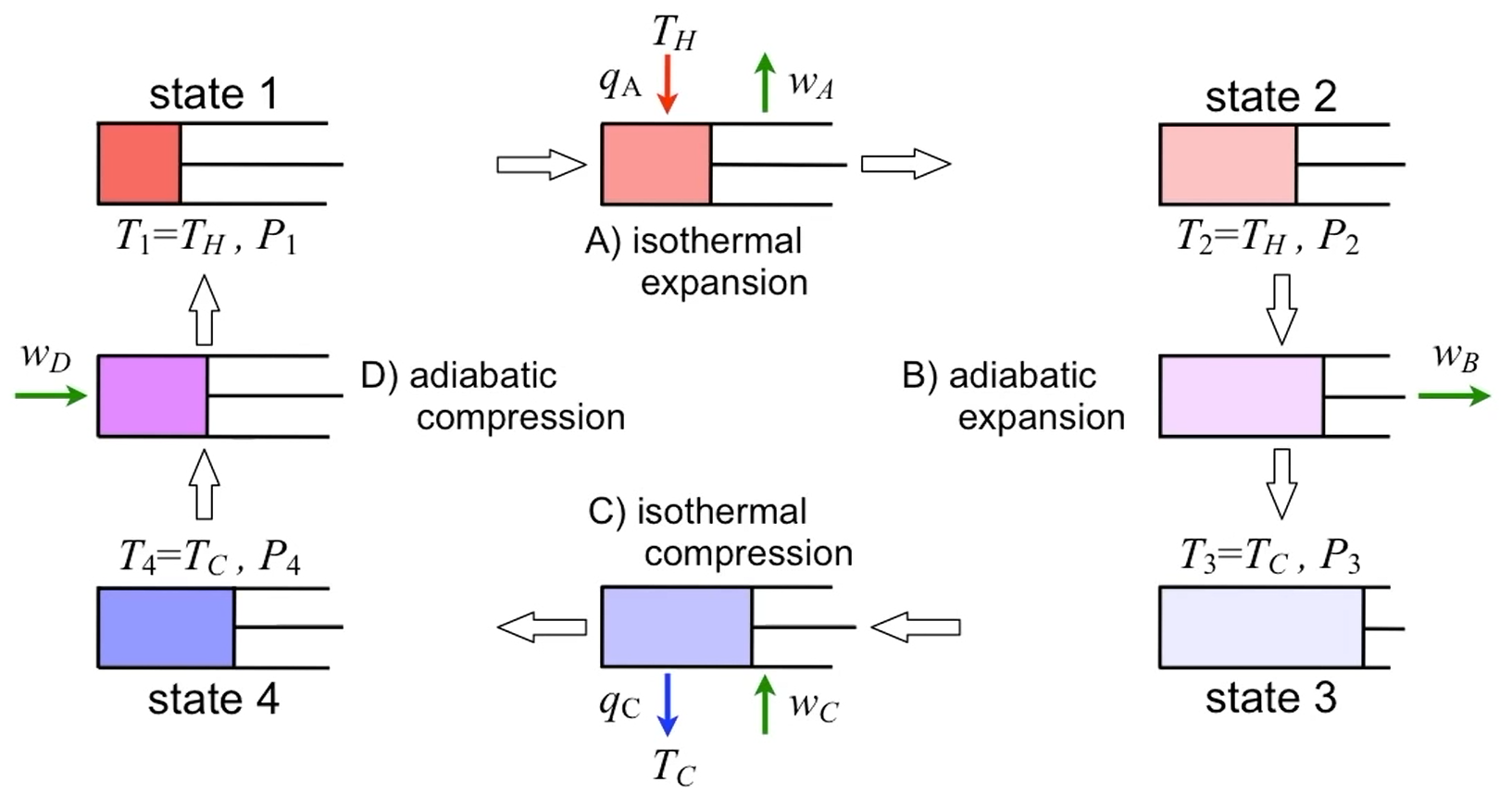
Net work −Wnet=∣W12∣+∣W23∣−∣W34∣−∣W41∣-W_{\text{net}} = \vert W_{12} \vert + \vert W_{23} \vert - \vert W_{34} \vert - \vert W_{41} \vert
Net work and heat −Wnet=∣QH∣−∣QC∣-W_{\text{net}} = \vert Q_H \vert - \vert Q_C \vert
Carnot efficiency η=1−THTC\eta = 1 - \dfrac{T_H}{T_C}
State properties after cycle Δucycle=0Δhcycle=0Δscycle=0\Delta u_{\text{cycle}} = 0 \newline \Delta h_{\text{cycle}} = 0 \newline \Delta s_{\text{cycle}} = 0
Entropy change of surrounding Δssurr=0=−qHTH−qCTC\Delta s_{\text{surr}} = 0 = -\dfrac{q_H}{T_H} -\dfrac{q_C}{T_C}

/cheme/cheme326/cheme-326-carnot-cycle.png
Carnot cycle. (Episode C1 - Process Efficiency by Stu Adler UW)
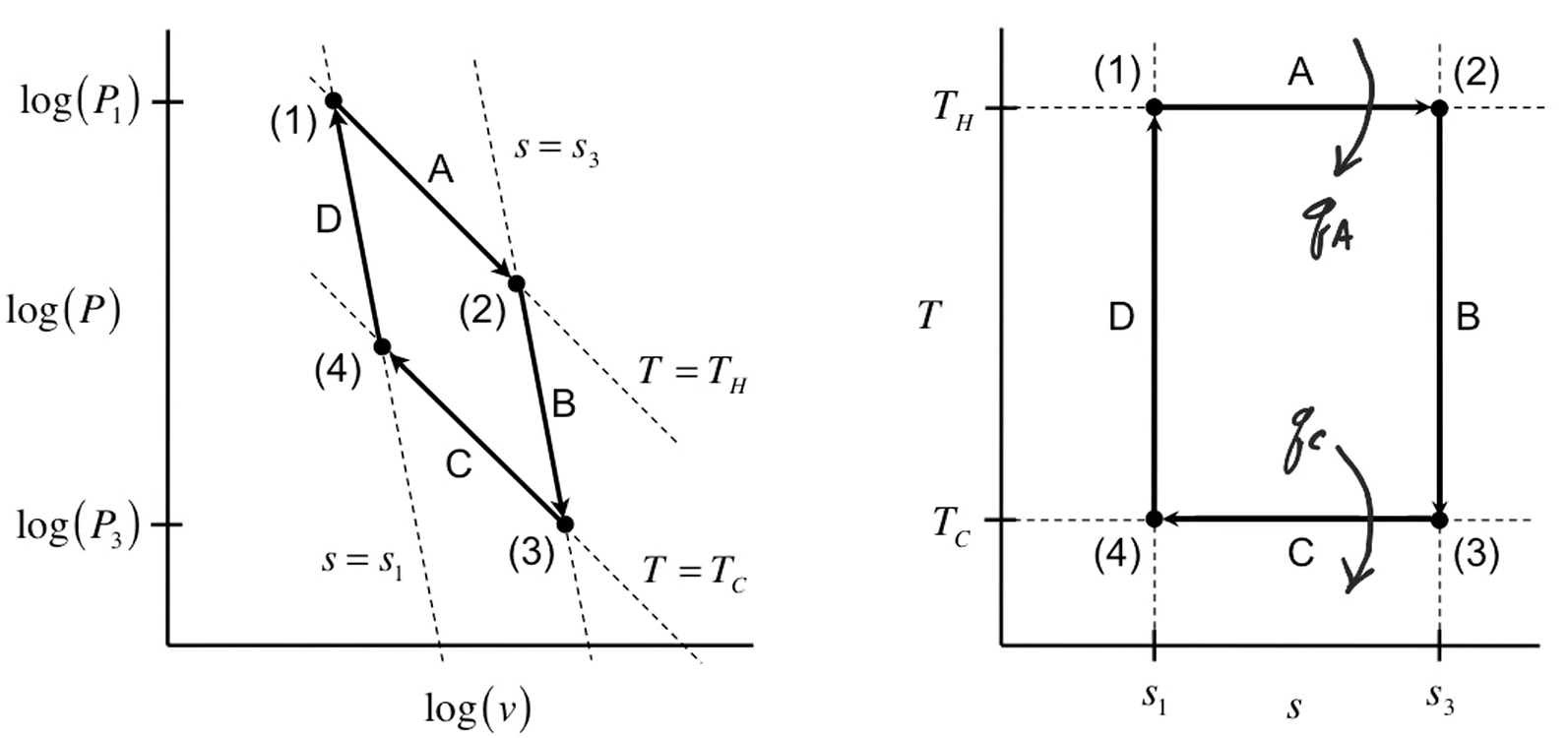
/cheme/cheme326/cheme-326-carnot-cycle-diagram.png
Carnot cycle diagrams. (Episode C1 - Process Efficiency by Stu Adler UW)

Description Equations
Open system balance 0=m˙1(h^+12v2+gz)1−m˙2(h^+12v2+gz)20 = \dot{m}_1 (\hat{h} + \frac{1}{2}v^2 + gz)_1 - \dot{m}_2 (\hat{h} + \frac{1}{2}v^2 + gz)_2
Shaft work w˙s=∫v dP+Δe˙K+Δe˙P\dot{w}_s = \int v \ dP + \Delta \dot{e}_K + \Delta \dot{e}_P
Nozzle, diffuser simplifications 0=ΔEP=Q˙=W˙s0 = \Delta E_P = \dot{Q} = \dot{W}_s
Turbine, pump, compressor simplifications 0=ΔEK=Q˙0 = \Delta E_K = \dot{Q}
Heat exchanger simplifications 0=ΔEP=ΔEK=W˙s0 = \Delta E_P = \Delta E_K = \dot{W}_s
Throttling device simplifications 0=ΔEP=ΔEK=Q˙=W˙s0 = \Delta E_P = \Delta E_K = \dot{Q} = \dot{W}_s
Description Equations
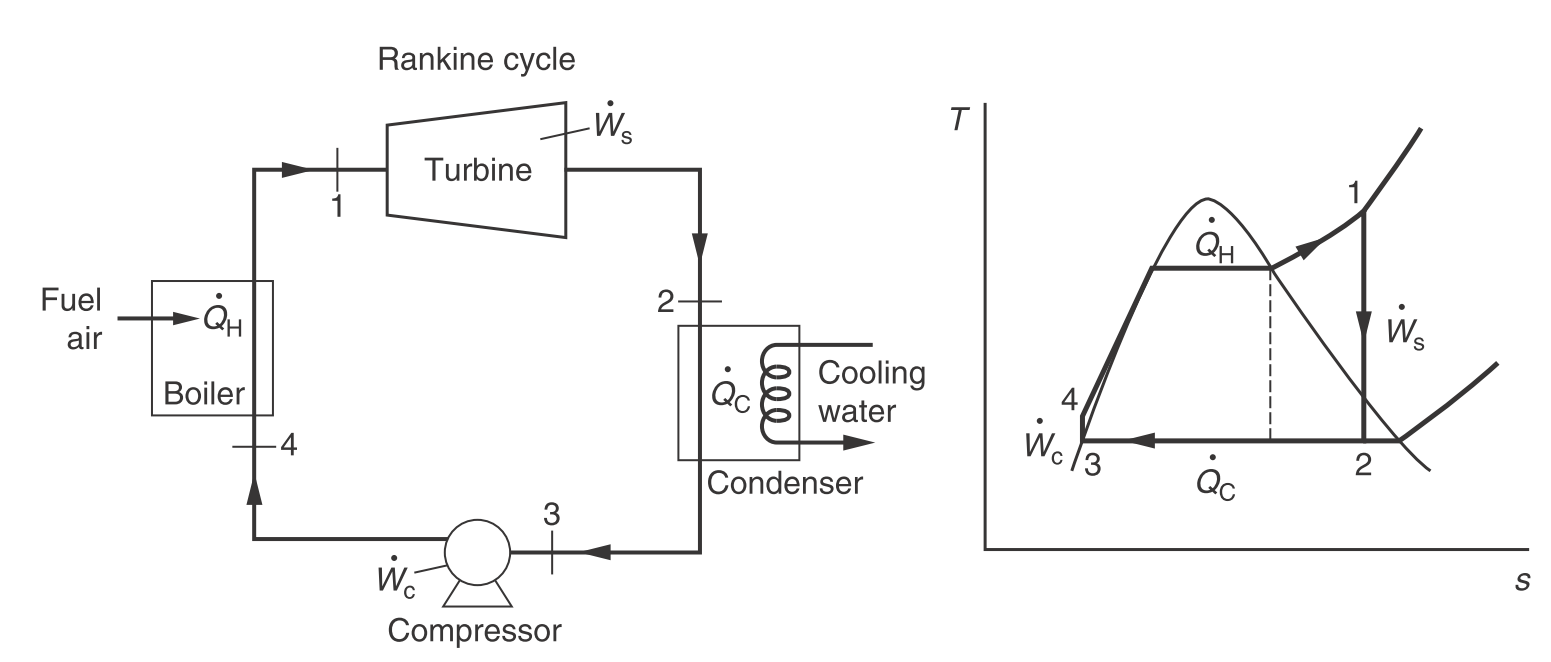
Turbine w˙s=h2−h1q˙=0\dot{w}_s = h_2 - h_1 \newline \dot{q} = 0
Condenser q˙=h3−h2w˙s=0\dot{q} = h_3 - h_2 \newline \dot{w}_s = 0
Compressor w˙c=h4−h3=vΔPq˙=0\dot{w}_c = h_4 - h_3 = v\Delta P \newline \dot{q} = 0
Boiler q˙=h1−h4w˙s=0\dot{q} = h_1 - h_4 \newline \dot{w}_s = 0
Efficiency η=∣w˙s∣−w˙cq˙h=∣h2−h1∣−(h4−h3)h1−h4\eta = \dfrac{\vert\dot{w}_s\vert - \dot{w}_c}{\dot{q}_h} = \dfrac{\vert h_2 - h_1 \vert - (h_4 - h_3)}{h_1 - h_4}
Net work w˙net=q˙H−∣q˙C∣=∣w˙s∣−w˙c\dot{w}_{\text{net}} = \dot{q}_H - \vert\dot{q}_C\vert = \vert\dot{w}_s\vert - \dot{w}_c
/cheme/cheme326/cheme-326-rankine-cycle.png
Ideal Rankine cycle. (Engineering and Chemical Thermodynamics 2e by Koretsky p164.)
Description Equations
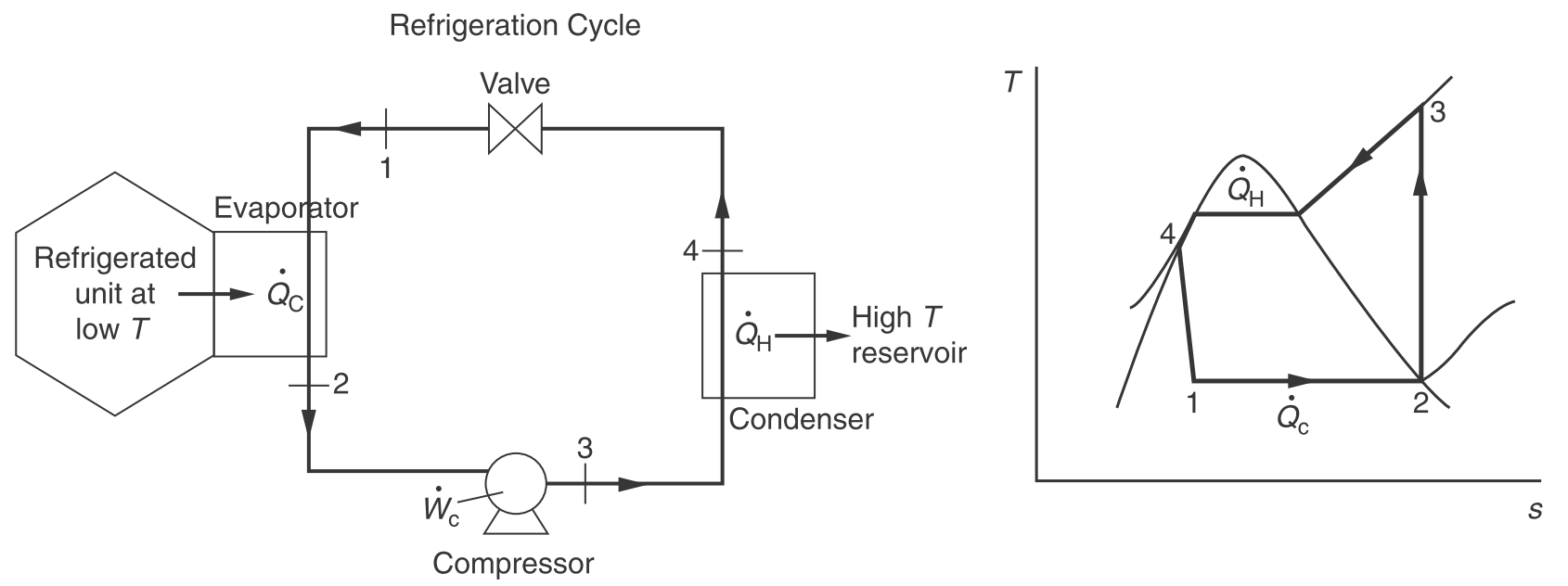
Evaporator q˙=h2−h1w˙s=0\dot{q} = h_2 - h_1 \newline \dot{w}_s = 0
Compressor w˙s=h3−h2q˙=0\dot{w}_s = h_3 - h_2 \newline \dot{q} = 0
Condenser q˙=h4−h3w˙s=0\dot{q} = h_4 - h_3 \newline \dot{w}_s = 0
Value w˙s=0q˙=0Δh=0Δs>0 (irreversible expansion)\dot{w}_s = 0 \newline \dot{q} = 0 \newline \Delta h = 0 \newline \Delta s > 0 \text{ (irreversible expansion)}
Coefficient of performance COP=Q˙CW˙c=h2−h1h3−h2\mathrm{COP} = \dfrac{\dot{Q}_C}{\dot{W}_c} = \dfrac{h_2 - h_1}{h_3 - h_2}
/cheme/cheme326/cheme-326-refrigeration-cycle.png
Ideal refrigeration cycle. (Engineering and Chemical Thermodynamics 2e by Koretsky p170.)
Description Equations
Conservative force Fij=−∇ΓijF_{ij} = -\nabla \Gamma_{ij}
Potential Γij=−∫Fij dr\Gamma_{ij} = -\int F_{ij} \ dr
Description Equations (SI unit)
Coulomb interaction
(electrostatic, point charges)		 Γij(r)=QiQj4πε01r\Gamma_{ij}(r) = \dfrac{Q_i Q_j}{4\pi\varepsilon_0}\dfrac{1}{r}
Dipole-dipole interaction
(polar, electric dipole, Keesom)		 Γij(r)=−(2)3μi2μj2(4πε0)21kT1r6\Gamma_{ij}(r) = -\dfrac{(2)}{3}\dfrac{\mu_i^2 \mu_j^2}{(4\pi\varepsilon_0)^2}\dfrac{1}{kT}\dfrac{1}{r^6}
Dipole-induced dipole interaction
(induction, Debye)		 Γij(r)=−αiμj2(4πε0)21r6\Gamma_{ij}(r) = -\dfrac{\alpha_i \mu_j^2}{(4\pi\varepsilon_0)^2}\dfrac{1}{r^6}
Induced dipole-induced dipole interaction
(dispersion, London)		 Γij(r)=−32αiαj(4πε0)2IiIjIi+Ij1r6\Gamma_{ij}(r) = -\dfrac{3}{2}\dfrac{\alpha_i \alpha_j}{(4\pi\varepsilon_0)^2}\dfrac{I_i I_j}{I_i + I_j}\dfrac{1}{r^6}
Description Equations (SI unit)
van der Waals interaction Γijvdw=ΓijK+ΓijD+ΓijL=−Cvdwr6\Gamma_{ij}^{\text{vdw}} = \Gamma_{ij}^{\text{K}} + \Gamma_{ij}^{\text{D}} + \Gamma_{ij}^{\text{L}} = -\dfrac{C_{\text{vdw}}}{r^6}
Keesom coefficient CK=(2)3μi2μj2(4πε0)21kTC^{\text{K}} = \dfrac{(2)}{3}\dfrac{\mu_i^2 \mu_j^2}{(4\pi\varepsilon_0)^2}\dfrac{1}{kT}
Debye coefficient CD=αiμj2+αjμi2(4πε0)2C^{\text{D}} = \dfrac{\alpha_i \mu_j^2 + \alpha_j \mu_i^2}{(4\pi\varepsilon_0)^2}
London coefficient CL=32αiαj(4πε0)2IiIjIi+IjC^{\text{L}} = \dfrac{3}{2}\dfrac{\alpha_i \alpha_j}{(4\pi\varepsilon_0)^2}\dfrac{I_i I_j}{I_i + I_j}
Description Equations (CGS unit)
Coulomb interaction
(electrostatic, point charges)		 Γij(r)=QiQjr\Gamma_{ij}(r) = \dfrac{Q_i Q_j}{r}
Dipole-dipole interaction
(polar, electric dipole, Keesom)		 Γij(r)=−(2)3μi2μj2kT1r6\Gamma_{ij}(r) = -\dfrac{(2)}{3}\dfrac{\mu_i^2 \mu_j^2}{kT}\dfrac{1}{r^6}
Dipole-induced dipole interaction
(induction, Debye)		 Γij(r)=−αiμj2r6\Gamma_{ij}(r) = -\dfrac{\alpha_i \mu_j^2}{r^6}
Induced dipole-induced dipole interaction
(dispersion, London)		 Γij(r)=−32αiαjr6IiIjIi+Ij\Gamma_{ij}(r) = -\dfrac{3}{2}\dfrac{\alpha_i \alpha_j}{r^6}\dfrac{I_i I_j}{I_i + I_j}
Description Equations (CGS unit)
van der Waals interaction Γijvdw=ΓijK+ΓijD+ΓijL=−Cvdwr6\Gamma_{ij}^{\text{vdw}} = \Gamma_{ij}^{\text{K}} + \Gamma_{ij}^{\text{D}} + \Gamma_{ij}^{\text{L}} = -\dfrac{C_{\text{vdw}}}{r^6}
Keesom coefficient CK=(2)3μi2μj2kTC^{\text{K}} = \dfrac{(2)}{3}\dfrac{\mu_i^2 \mu_j^2}{kT}
Debye coefficient CD=αiμj2+αjμi2C^{\text{D}} = \alpha_i \mu_j^2 + \alpha_j \mu_i^2
London coefficient CL=32αiαjIiIjIi+IjC^{\text{L}} = \dfrac{3}{2}\alpha_i \alpha_j\dfrac{I_i I_j}{I_i + I_j}
Description Equations (SI unit)
Hard sphere model Γ={0r>σ∞r≤σ\Gamma = \begin{cases} 0 & r > \sigma \\ \infty & r \le \sigma \end{cases}
Surtherland model Γ={−Cvdwr6r>σ∞r≤σ\Gamma = \begin{cases} -\dfrac{C_{\text{vdw}}}{r^6} & r > \sigma \\ \infty & r \le \sigma \end{cases}
Lennard-Jones potential Γ=Crepr12−Cvdwr6\Gamma = \dfrac{C_{\text{rep}}}{r^{12}} - \dfrac{C_{\text{vdw}}}{r^6}
Lennard-Jones potential Γ=4ε[(σr)12−(σr)6]\Gamma = 4\varepsilon \left[ \left(\dfrac{\sigma}{r}\right)^{12} - \left(\dfrac{\sigma}{r}\right)^6 \right]
Description Equations
Ideal gas law Pv=RTPv = RT
Compressibility factor z=PvRTz = \dfrac{Pv}{RT}
Reduced temperature Tr=TTcT_r = \dfrac{T}{T_c}
Reduced pressure Pr=PPcP_r = \dfrac{P}{P_c}
Pitzer acentric factor ω=−1−log⁡10[Prsat(Tr=0.7)]\omega = -1 - \log_{10} [P_r^{\text{sat}}(T_r = 0.7)]
Generalized compressibility z=z(0)+ωz(1)z = z^{(0)} + \omega z^{(1)}
Description Equations
van der Waals EOS
(pressure explicit form)		 P=RTv−b−av2P = \dfrac{RT}{v-b} - \dfrac{a}{v^2}
van der Waals EOS
(cubic form)		 Pv3−(RT+Pb)v2+av−ab=0Pv^3 - (RT + Pb)v^2 + av - ab = 0
van der Waals EOS
(reduced form)		 P=8Tr3vr−1−3vr2P = \dfrac{8T_r}{3v_r - 1} - \dfrac{3}{v_r^2}
Intermolecular force (pressure) correction a=2764(RTc)2Pca = \dfrac{27}{64}\dfrac{(RT_c)^2}{P_c}
Volume correction b=RTc8Pcb = \dfrac{RT_c}{8P_c}
Critical compressibility factor zc=38z_c = \frac{3}{8}
Description Equations
Redlich-Kwong EOS P=RTv−b−aTv(v+b)P = \dfrac{RT}{v-b} - \dfrac{a}{\sqrt{T}v(v+b)}
Intermolecular force (pressure) correction a=0.42748R2Tc2.5Pca = 0.42748 \dfrac{R^2 T_c^{2.5}}{P_c}
Volume correction b=0.08664RTcPcb = 0.08664 \dfrac{RT_c}{P_c}
Critical compressibility factor zc=13z_c = \frac{1}{3}
Description Equations
Peng-Robinson EOS P=RTv−b−aα(T)v(v+b)+b(v−b)P = \dfrac{RT}{v-b} - \dfrac{a \alpha(T)}{v(v+b) + b(v-b)}
Intermolecular force (pressure) correction a=0.45724R2Tc2Pca = 0.45724 \dfrac{R^2 T_c^{2}}{P_c}
Volume correction b=0.07780RTcPcb = 0.07780 \dfrac{RT_c}{P_c}
Constant α(T)=[1+κ(1−Tr)]2\alpha(T) = [1 + \kappa(1 - \sqrt{T_r})]^2
Constant κ=0.37464+1.54226ω−0.26992ω2\kappa = 0.37464 + 1.54226\omega - 0.26992\omega^2
Critical compressibility factor zc=0.307z_c = 0.307
Description Equations
Virial EOS z=PvRT=1+Bv+Cv2+Dv3+⋯z = \dfrac{Pv}{RT} = 1 + \dfrac{B}{v} + \dfrac{C}{v^2} + \dfrac{D}{v^3} + \cdots
Second virial coefficient B=RTcBrPcB = \dfrac{RT_c B_r}{P_c}
Reduced second virial coefficient Br=B(0)+ωB(1)B_r = B^{(0)} + \omega B^{(1)}
0th order correction B(0)=0.083−0.422Tr1.6B^{(0)} = 0.083 - \dfrac{0.422}{T_r^{1.6}}
1st order correction B(1)=0.139−0.172Tr4.2B^{(1)} = 0.139 - \dfrac{0.172}{T_r^{4.2}}
Description Equations
aa for binary mixtures amix=y12a1+2y1y2a12+y22a2a_{\text{mix}} = y_1^2 a_1 + 2 y_1y_2 a_{12} + y_2^2 a_2
aa of different species interaction a12=a1a2(1−k12)a_{12} = \sqrt{a_1 a_2}(1 - k_{12})
bb for binary mixtures bmix=y1b1+y2b2b_{\text{mix}} = y_1b_1 + y_2b_2
aa for multicomponent mixtures amix=∑i∑jyiyjaija_{\text{mix}} = \sum\limits_i\sum\limits_j y_i y_j a_{ij}
bb for multicomponent mixtures bmix=∑iyibib_{\text{mix}} = \sum\limits_i y_i b_{i}
Description Equations
Second virial coefficient for binary mixture Bmix=y12B11+2y1y2B12+y22B22B_{\text{mix}} = y_1^2 B_{11} + 2 y_1 y_2 B_{12} + y_2^2 B_{22}
Second virial coefficient for multicomponent mixture Bmix=∑i∑jyiyjBijB_{\text{mix}} = \sum\limits_i\sum\limits_j y_i y_j B_{ij}
Third virial coefficient for multicomponent mixture Cmix=∑i∑j∑kyiyjykCijkC_{\text{mix}} = \sum\limits_i\sum\limits_j\sum\limits_k y_i y_j y_k C_{ijk}
Description Equations
Pseudocritical temperature Tpc=∑yiTc,iT_{pc} = \sum y_i T_{c, i}
Pseudocritical pressure Ppc=∑yiPc,iP_{pc} = \sum y_i P_{c, i}
Pseudocritical acentric factor ωpc=∑yiωc,i\omega_{pc} = \sum y_i \omega_{c, i}
Description Equations
Thermal expansion coefficient β=1v(∂v∂T)P\beta = \dfrac{1}{v} \left(\dfrac{\partial v}{\partial T}\right)_P
Isothermal compressibility κ=−1v(∂v∂P)T\kappa = -\dfrac{1}{v} \left(\dfrac{\partial v}{\partial P}\right)_T
Rackett equation vlsat=RTcPc(0.29056−0.08775ω)(1+(1−Tr)2/7)v_l^{\text{sat}} = \dfrac{RT_c}{P_c} (0.29056 - 0.08775 \omega)^{(1 + (1 - T_r)^{2/7})}
Description Equations
Total differential dz=(∂z∂x)ydx+(∂z∂y)xdydz = \left(\dfrac{\partial z}{\partial x}\right)_y dx + \left(\dfrac{\partial z}{\partial y}\right)_x dy
Clairaut’s theorem
Symmetry of second derivative		 ∂∂x(∂z∂y)=∂∂y(∂z∂x)\dfrac{\partial}{\partial x} \left(\dfrac{\partial z}{\partial y} \right) = \dfrac{\partial}{\partial y} \left( \dfrac{\partial z}{\partial x} \right)
Chain rule ∂z∂x=∂z∂y∂y∂x\dfrac{\partial z}{\partial x} = \dfrac{\partial z}{\partial y}\dfrac{\partial y}{\partial x}
Cyclic relation
Triple chain rule		 (∂x∂y)z(∂y∂z)x(∂z∂x)y=−1\left(\dfrac{\partial x}{\partial y}\right)_z \left(\dfrac{\partial y}{\partial z}\right)_x \left(\dfrac{\partial z}{\partial x}\right)_y = -1
Relations Internal energy uu Enthalpy hh Helmholz energy aa Gibbs energy gg
Definition - h=u+Pvh = u + Pv a=u−Tsa = u - Ts g=h−Tsg = h - Ts
Fundamental property relations du=Tds−Pdvdu = Tds - Pdv dh=Tds+vdPdh = Tds + vdP da=−sdT−Pdvda = -sdT - Pdv dg=−sdT+vdPdg = -sdT + vdP
Fundamental grouping {u,s,v}\lbrace u, s, v \rbrace {h,s,P}\lbrace h, s, P \rbrace {a,T,v}\lbrace a, T, v \rbrace {g,T,P}\lbrace g, T, P \rbrace
Fundamental grouping relations (∂u∂s)v=T\left(\frac{\partial u}{\partial s}\right)_v = T (∂h∂s)P=T\left(\frac{\partial h}{\partial s}\right)_P = T (∂a∂T)v=−s\left(\frac{\partial a}{\partial T}\right)_v = -s (∂g∂T)P=−s\left(\frac{\partial g}{\partial T}\right)_P = -s
Fundamental grouping relations (∂u∂v)s=−P\left(\frac{\partial u}{\partial v}\right)_s = -P (∂h∂P)s=v\left(\frac{\partial h}{\partial P}\right)_s = v (∂a∂v)T=−P\left(\frac{\partial a}{\partial v}\right)_T = -P (∂g∂P)T=v\left(\frac{\partial g}{\partial P}\right)_T = v
Maxwell’s relations (∂T∂v)s=−(∂P∂s)v\left(\frac{\partial T}{\partial v}\right)_s = -\left(\frac{\partial P}{\partial s}\right)_v (∂T∂P)s=(∂v∂s)P\left(\frac{\partial T}{\partial P}\right)_s = \left(\frac{\partial v}{\partial s}\right)_P (∂s∂v)T=(∂P∂T)v\left(\frac{\partial s}{\partial v}\right)_T = \left(\frac{\partial P}{\partial T}\right)_v (∂s∂P)T=−(∂v∂T)P\left(\frac{\partial s}{\partial P}\right)_T = -\left(\frac{\partial v}{\partial T}\right)_P
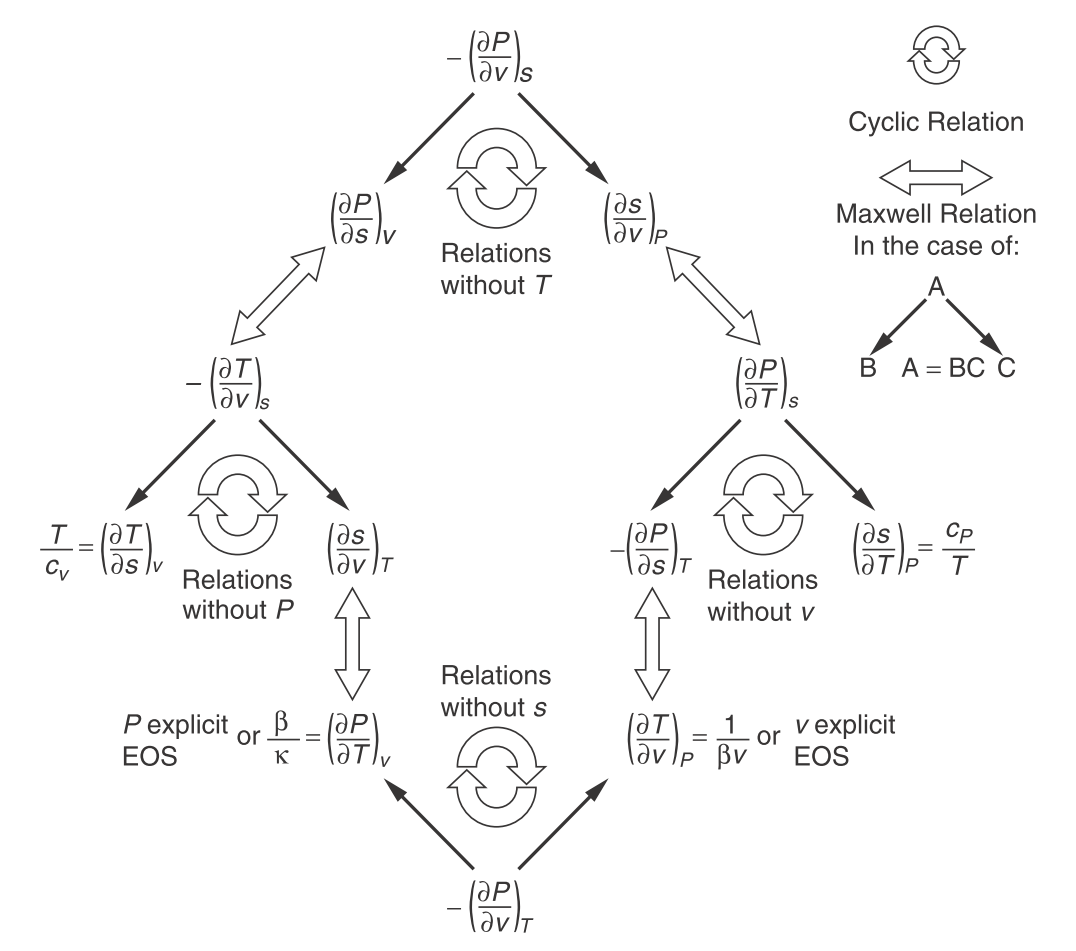
/cheme/cheme326/cheme-326-thermodynamic-relations.png
Thermodynamic relations. (Engineering and Chemical Thermodynamics 2e by Koretsky p274.)
Description Equations
Constant volume heat capacity cv=(∂u∂T)v=T(∂s∂T)vc_v = \left(\dfrac{\partial u}{\partial T}\right)_v = T \left(\dfrac{\partial s}{\partial T}\right)_v
Constant pressure heat capacity cP=(∂h∂T)P=T(∂s∂T)Pc_P = \left(\dfrac{\partial h}{\partial T}\right)_P = T \left(\dfrac{\partial s}{\partial T}\right)_P
Constant volume heat capacity of real gas cvreal=cvideal+∫videalvreal[T(∂2P∂T2)v]dvc_v^{\text{real}} = c_v^{\text{ideal}} + \displaystyle\int_{v_{\text{ideal}}}^{v_{\text{real}}} \left[T \left(\dfrac{\partial^2 P}{\partial T^2}\right)_v\right] dv
Constant pressure heat capacity of real gas cPreal=cPideal−∫PidealPreal[T(∂2v∂T2)P]dPc_P^{\text{real}} = c_P^{\text{ideal}} - \displaystyle\int_{P_{\text{ideal}}}^{P_{\text{real}}} \left[T \left(\dfrac{\partial^2 v}{\partial T^2}\right)_P\right] dP
Thermal expansion coefficient β=1v(∂v∂T)P\beta = \dfrac{1}{v} \left(\dfrac{\partial v}{\partial T}\right)_P
Thermal expansion coefficient of ideal gas β=1T\beta = \dfrac{1}{T}
Isothermal compressibility κ=−1v(∂v∂P)T\kappa = -\dfrac{1}{v} \left(\dfrac{\partial v}{\partial P}\right)_T
Isothermal compressibility of ideal gas κ=1P\kappa = \dfrac{1}{P}
Description Equations
Entropy change s(T,v)s(T, v) ds=cvTdT+(∂P∂T)vdvds = \dfrac{c_v}{T} dT + \left(\dfrac{\partial P}{\partial T}\right)_v dv
Entropy change s(T,P)s(T, P) ds=cPTdT+(∂v∂T)PdPds = \dfrac{c_P}{T} dT + \left(\dfrac{\partial v}{\partial T}\right)_P dP
Internal energy change u(T,v)u(T, v) du=cvdT+[T(∂P∂T)v−P]dvdu = c_v dT + \left[T \left(\dfrac{\partial P}{\partial T}\right)_v - P\right] dv
Enthalpy change h(T,P)h(T, P) dh=cPdT+[−T(∂v∂T)P+v]dPdh = c_P dT + \left[-T \left(\dfrac{\partial v}{\partial T}\right)_P + v\right] dP
General f(T,P)f(T, P) Ideal gas β=1T,κ=1P\beta = \frac{1}{T}, \kappa = \frac{1}{P}
ds=cPTdT−βv dPds = \dfrac{c_P}{T} dT - \beta v \ dP ds=cPTdT−RPdPds = \dfrac{c_P}{T} dT - \dfrac{R}{P} dP
dv=βv dT−κv dPdv = \beta v \ dT - \kappa v \ dP dv=vTdT−vPdPdv = \dfrac{v}{T}dT - \dfrac{v}{P}dP
du=(cP−βPv)dT+(κPv−βvT)dPdu = (c_P - \beta Pv)dT + (\kappa Pv - \beta vT)dP du=(cP−R)dTdu = (c_P - R)dT
dh=(cP−βPv)dT+v dPdh = (c_P - \beta Pv)dT + v \ dP dh=cP dTdh = c_P \ dT
da=−s dT+(κPv−βvT)dPda = -s \ dT + (\kappa Pv - \beta vT)dP da=−s dTda = -s \ dT
dg=−s dT+v dPdg = -s \ dT + v \ dP dg=−s dT+v dPdg = -s \ dT + v \ dP
Description Equations
General departure function dep=real−ideal\mathrm{dep = real - ideal}
Enthalpy departure function Δhdep=hreal−hideal\Delta h^{\text{dep}} = h^{\text{real}} - h^{\text{ideal}}
Entropy departure function Δsdep=sreal−sideal\Delta s^{\text{dep}} = s^{\text{real}} - s^{\text{ideal}}
Dimensionless enthalpy departure function ΔhdepRTc=Tr2∫0P[−1Pr(∂z∂Tr)P]dPr\dfrac{\Delta h^{\text{dep}}}{RT_c} = T_r^2 \displaystyle\int_0^P \left[-\dfrac{1}{P_r}\left(\dfrac{\partial z}{\partial T_r}\right)_P \right] dP_r
Dimensionless entropy departure function ΔsdepR=∫0P−[z−1Pr+TrPr(∂z∂Tr)P]dPr\dfrac{\Delta s^{\text{dep}}}{R} = \displaystyle\int_0^P -\left[\dfrac{z-1}{P_r} + \dfrac{T_r}{P_r}\left(\dfrac{\partial z}{\partial T_r}\right)_P \right] dP_r
Dimensionless enthalpy departure function with Lee-Kesler EOS ΔhdepRTc=[ΔhdepRTc](0)+ω[ΔhdepRTc](1)\dfrac{\Delta h^{\text{dep}}}{RT_c} = \left[\dfrac{\Delta h^{\text{dep}}}{RT_c}\right]^{(0)} + \omega \left[\dfrac{\Delta h^{\text{dep}}}{RT_c}\right]^{(1)}
Dimensionless entropy departure function with Lee-Kesler EOS ΔsdepR=[ΔsdepR](0)+ω[ΔsdepR](1)\dfrac{\Delta s^{\text{dep}}}{R} = \left[\dfrac{\Delta s^{\text{dep}}}{R}\right]^{(0)} + \omega \left[\dfrac{\Delta s^{\text{dep}}}{R}\right]^{(1)}
Description Equations
Joule-Thomson expansion
Adiabatic reversible throttling		 q˙=0w˙s=0Δh=0\dot{q} = 0 \newline \dot{w}_s = 0 \newline \Delta h = 0
Joule-Thomson coefficient μJT=(∂T∂P)h\mu_{\text{JT}} = \left(\dfrac{\partial T}{\partial P}\right)_h
Joule-Thomson coefficient μJT=[−T(∂v∂T)P+v]cPreal\mu_{\text{JT}} = \dfrac{\left[-T \left(\dfrac{\partial v}{\partial T}\right)_P + v\right]}{c_P^{\text{real}}}
Description Equations
Gibbs free energy g=h−Tsg = h - Ts
Second law of thermodynamics dGi≤0dG_i \le 0
Criteria for chemical equilibrium giα=giβg_i^\alpha = g_i^\beta
Clapeyron equation
General phase equilibrium		 dPdT=ΔsΔv=ΔhTΔv\dfrac{dP}{dT} = \dfrac{\Delta s}{\Delta v} = \dfrac{\Delta h}{T\Delta v}
Clausius-Clapeyron equation
★ Vapor-liquid equilibrium
★ Ideal gas, negligible liquid volume		 dPsatPsat=ΔhvapdTRT2\dfrac{dP^{\text{sat}}}{P^{\text{sat}}} = \dfrac{\Delta h_{\text{vap}} dT}{RT^2}
Clausius-Clapeyron equation
★ Vapor-liquid equilibrium
★ Ideal gas, negligible liquid volume
★ Δhvap\Delta h_{\text{vap}} independent of TT		 ln⁡P2satP1sat=−ΔhvapR(1T2−1T1)\ln\dfrac{P_2^{\text{sat}}}{P_1^{\text{sat}}} = -\dfrac{\Delta h_{\text{vap}}}{R} \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right)
Antoine’s equation ln⁡Psat=A−BC+T\ln P^{\text{sat}} = A - \dfrac{B}{C+T}
Description Equations
Extensive total solution (mixture) property KK
Intensive total solution (mixture) property k=Knk = \dfrac{K}{n}
Extensive pure species property KiK_i
Intensive pure species property ki=Kinik_i = \dfrac{K_i}{n_i}
Partial molar property K‾i=(∂K∂ni)T,P,nj≠i\overline{K}_i = \left(\dfrac{\partial K}{\partial n_i}\right)_{T, P, n_{j\not= i}}
Limiting case of partial molar property lim⁡xi→1K‾i=kilim⁡xi→0K‾i=K‾i∞\displaystyle\lim_{x_i \to 1} \overline{K}_i = k_i \newline \lim_{x_i \to 0} \overline{K}_i = \overline{K}_i^\infty
Differential of extensive property dK=(∂K∂T)P,nidT+(∂K∂P)T,nidP+∑K‾idnidK = \left(\frac{\partial K}{\partial T}\right)_{P, n_i} dT + \left(\frac{\partial K}{\partial P}\right)_{T, n_i} dP + \sum \overline{K}_i dn_i
Relation between properties
★ Constant T, P		 K=∑niK‾ik=∑xiK‾iK = \sum n_i \overline{K}_i \newline k = \sum x_i \overline{K}_i
Gibbs-Duhem equation
★ Constant T, P		 ∑nidK‾i=0\sum n_i d\overline{K}_i = 0
Corollary of Gibbs-Duhem equation
★ Binary mixture		 x1dK1‾dx1+x2dK2‾dx1=0x_1 \dfrac{d\overline{K_1}}{d x_1} + x_2 \dfrac{d\overline{K_2}}{d x_1} = 0
Description Equations
Extensive property change of mixing ΔKmix=K−∑nikiΔKmix=∑ni(K‾i−ki)\Delta K_{\text{mix}} = K - \sum n_i k_i \newline \Delta K_{\text{mix}} = \sum n_i (\overline{K}_i - k_i)
Intensive property change of mixing Δkmix=k−∑xikiΔkmix=∑xi(K‾i−ki)\Delta k_{\text{mix}} = k - \sum x_i k_i \newline \Delta k_{\text{mix}} = \sum x_i (\overline{K}_i - k_i)
Enthalpy of mixing Δhmix=∑xi(h‾i−hi)\Delta h_{\text{mix}} = \sum x_i (\overline{h}_i - h_i)
Enthalpy of mixing Δhmix=Δh~sn+1=Δh~sx1\Delta h_{\text{mix}} = \dfrac{\Delta \tilde{h}_s}{n+1} = \Delta \tilde{h}_s x_1
Enthalpy of solution Δh~s=Δhmixx1=Δhmix(n+1)\Delta \tilde{h}_s = \dfrac{\Delta h_{\text{mix}}}{x_1} = \Delta h_{\text{mix}}(n+1)
Entropy of mixing
★ Ideal gas, regular solution		 Δsmix=−R∑yiln⁡yi\Delta s_{\text{mix}} = -R\sum y_i \ln y_i
Partial molar property change of mixing ΔK‾mix,i=K‾i−ki\overline{\Delta K}_{\text{mix}, i} = \overline{K}_i - k_i
Description Equations
Partial molar volume of species 1
★ Virial EOS		 V‾1=RTP+(y12+2y1y2)B11+2y22B12−y22B22\overline{V}_1 = \dfrac{RT}{P} + (y_1^2 + 2y_1 y_2)B_{11} + 2y_2^2 B_{12} - y_2^2 B_{22}
Partial molar volume of species 2
★ Virial EOS		 V‾2=RTP−y12B11+2y12B12+(y22+2y1y2)B22\overline{V}_2 = \dfrac{RT}{P} - y_1^2 B_{11} + 2y_1^2 B_{12} + (y_2^2 + 2y_1 y_2)B_{22}
Volume change of mixing
★ Virial EOS		 Δvmix=y1y2(2B12−B11−B22)\Delta v_{\text{mix}} = y_1 y_2(2B_{12} - B_{11} - B_{22})
Partial molar property K‾i=ki+ΔK‾mix,i\overline{K}_i = k_i + \overline{\Delta K}_{\text{mix}, i}
Graphical method
Slope is difference		 dkdx1=K‾1−K‾2\dfrac{dk}{dx_1} = \overline{K}_1 - \overline{K}_2
Graphical method
K‾2\overline{K}_2 is intercept		 k=x1dkdx1+K‾2k = x_1 \dfrac{dk}{dx_1} + \overline{K}_2
Graphical method
K‾2\overline{K}_2 explicit		 K‾2=k−x1dkdx1\overline{K}_2 = k - x_1 \dfrac{dk}{dx_1}
Description Equations
Partial molar Gibbs energy dependence on temperature (∂G‾i∂T)P,ni=−S‾i\left(\dfrac{\partial \overline{G}_i}{\partial T}\right)_{P, n_i} = -\overline{S}_i
Partial molar Gibbs energy dependence on temperature (measurable) [∂∂T(G‾iT)]P,ni=−H‾iT2\left[\dfrac{\partial}{\partial T}\left(\dfrac{\overline{G}_i}{T}\right)\right]_{P, n_i} = -\dfrac{\overline{H}_i}{T^2}
Partial molar Gibbs energy dependence on pressure (∂G‾i∂P)T,ni=−V‾i\left(\dfrac{\partial \overline{G}_i}{\partial P}\right)_{T, n_i} = -\overline{V}_i
Description Equations
Chemical potential μi=G‾i=(∂G∂ni)T,P,nj≠i\mu_i = \overline{G}_i = \left(\dfrac{\partial G}{\partial n_i}\right)_{T, P, n_{j \not= i}}
Criteria for chemical equilibrium μiα=μiβ\mu_i^\alpha = \mu_i^\beta
General multicomponent equilibrium Δ[−H‾iT2dT−V‾iTdP+1T[∂μi∂xi]T,Pdxi]=0\Delta \left[ -\dfrac{\overline{H}_i}{T^2}dT - \dfrac{\overline{V}_i}{T}dP + \dfrac{1}{T} \left[\dfrac{\partial \mu_i}{\partial x_i}\right]_{T, P} dx_i \right] = 0
Vapor liquid equilibrium
★ Ideal gas		 −hivT2dT−RdPP+Rdxivxiv=−H‾ilT2dT−V‾ilTdP+1T[∂μil∂xi]T,Pdxi\begin{aligned} &-\dfrac{h_i^v}{T^2}dT - R\dfrac{dP}{P} + R\dfrac{dx_i^v}{x_i^v} = -\dfrac{\overline{H}_i^l}{T^2}dT - \dfrac{\overline{V}_i^l}{T}dP + \dfrac{1}{T} \left[\dfrac{\partial \mu_i^l}{\partial x_i}\right]_{T, P} dx_i \end{aligned}
Description Equations
Definition of fugacity of pure species
★ Constant T		 gi−gi∘=RTln⁡(fifi∘)lim⁡P→0φi=1g_i - g_i^\circ = RT\ln\left(\dfrac{f_i}{f_i^\circ}\right) \newline \lim\limits_{P \to 0} \varphi_i = 1
Fugacity of pure species
★ Constant T		 fi=φiPf_i = \varphi_i P
Fugacity coefficient of pure species φi=fiP\varphi_i = \dfrac{f_i}{P}
Definition of fugacity of species i in mixture μi−μi∘=RTln⁡(f^if^i∘)lim⁡P→0φ^i=1\mu_i - \mu_i^\circ = RT\ln\left(\dfrac{\hat{f}_i}{\hat{f}_i^\circ}\right) \newline \lim\limits_{P \to 0} \hat{\varphi}_i = 1
Fugacity of species i in mixture f^i=yiPφ^i\hat{f}_i = y_i P \hat{\varphi}_i
Fugacity coefficient of species i in mixture
★ Constant T		 φ^i=f^ipi=f^iyiP\hat{\varphi}_i = \dfrac{\hat{f}_i}{p_i} = \dfrac{\hat{f}_i}{y_i P}
Criteria for chemical equilibrium f^iα=f^iβ\hat{f}_i^\alpha = \hat{f}_i^\beta
Description Equations
Reference state
★ Ideal gas		 P∘=PlowT∘=Tsysf^i∘=P∘P^\circ = P_{\text{low}} \newline T^\circ = T_{\text{sys}} \newline \hat{f}_i^\circ = P^\circ
Fugacity of pure species
★ Constant T		 fi=φiPf_i = \varphi_i P
Fugacity coefficient of pure species φi=fiP\varphi_i = \dfrac{f_i}{P}
Fugacity from experimental data fiv=P∘exp⁡(gi−gi∘RT)f_i^v = P^\circ \exp\left(\dfrac{g_i - g_i^\circ}{RT}\right)
Fugacity coefficient from experimental data φi=P∘Pexp⁡(gi−gi∘RT)\varphi_i = \dfrac{P^\circ}{P} \exp\left(\dfrac{g_i - g_i^\circ}{RT}\right)
Fugacity from EOS RTln⁡(fivP∘)=∫P∘Pvi dPRT\ln\left(\dfrac{f_i^v}{P^\circ}\right) = \displaystyle\int_{P^\circ}^P v_i \ dP
Fugacity coefficient from EOS φi=P∘Pexp⁡[1RT∫P∘Pvi dP]\varphi_i = \dfrac{P^\circ}{P} \exp\left[\dfrac{1}{RT}\displaystyle\int_{P^\circ}^P v_i \ dP\right]
Fugacity coefficient from vdW EOS ln⁡φiv=−ln⁡[(vi−b)PRT]+bvi−b−2aRTvi\ln\varphi_i^v = -\ln\left[\dfrac{(v_i - b)P}{RT}\right] + \dfrac{b}{v_i - b} - \dfrac{2a}{RTv_i}
Fugacity coefficient from virial form of vdW EOS ln⁡φiv=(b−aRT)PRT\ln\varphi_i^v = \left(b - \dfrac{a}{RT}\right) \dfrac{P}{RT}
Fugacity coefficient from generalized correlations ln⁡φiv=∫P∘P(zi−1)dPP\ln \varphi_i^v = \displaystyle\int_{P^\circ}^P (z_i - 1) \dfrac{dP}{P}
Generalized fugacity coefficient with Lee-Kesler EOS log⁡φi=log⁡φ(0)+ωlog⁡φ(1)\log\varphi_i = \log\varphi^{(0)} + \omega \log\varphi^{(1)}
Description Equations
Reference state
★ Ideal gas		 P∘=PlowT∘=Tsysni∘=ni,sysfi∘=yiP∘V∘=nRTP∘P^\circ = P_{\text{low}} \newline T^\circ = T_{\text{sys}} \newline n_i^\circ = n_{i, \text{sys}} \newline f_i^\circ = y_i P^\circ \newline V^\circ = \dfrac{nRT}{P^\circ}
Fugacity of species i in mixture
★ EOS
★ Full i-j interaction		 f^i=yiφ^iP\hat{f}_i = y_i \hat{\varphi}_i P
Fugacity of species i in mixture
★ Lewis fugacity rule
★ Same species interaction only, i-i interaction		 f^i=yiφiPφ^i=φi\hat{f}_i = y_i \varphi_i P \newline \hat{\varphi}_i = \varphi_i
Fugacity of species i in mixture
★ Ideal gas, no interaction		 f^i=yiPφ^i=1\hat{f}_i = y_i P \newline \hat{\varphi}_i = 1
Fugacity coefficient of species i in mixture
★ Constant T		 φ^i=f^ipi=f^iyiP\hat{\varphi}_i = \dfrac{\hat{f}_i}{p_i} = \dfrac{\hat{f}_i}{y_i P}
Fugacity coefficient from v-explicit EOS φ^i=P∘Pexp⁡[1RT∫P∘PV‾i dP]\hat{\varphi}_i = \dfrac{P^\circ}{P} \exp\left[\dfrac{1}{RT}\displaystyle\int_{P^\circ}^P \overline{V}_i \ dP\right]
Fugacity coefficient from P-explicit EOS φ^i=P∘Pexp⁡[−1RT∫V∘VP‾i dV]\hat{\varphi}_i = \dfrac{P^\circ}{P} \exp\left[-\dfrac{1}{RT}\displaystyle\int_{V^\circ}^V \overline{P}_i \ dV\right]
Description van der Waals EOS
Pure species i ln⁡φi=bivi−bi−ln⁡((vi−bi)PRT)−2aiRTvi\ln \varphi_{i}=\dfrac{b_{i}}{v_{i}-b_{i}}-\ln \left(\dfrac{\left(v_{i}-b_{i}\right) P}{R T}\right)-\dfrac{2 a_{i}}{R T v_{i}}
Species 1 in a binary mixture ln⁡φ^1=b1v−b−ln⁡((v−b)PRT)−2(y1a1+y2a12)RTv\ln \hat{\varphi}_{1}=\dfrac{b_{1}}{v-b}-\ln \left(\dfrac{(v-b) P}{R T}\right)-\dfrac{2\left(y_{1} a_{1}+y_{2} a_{12}\right)}{R T v}
Species i in a mixture ln⁡φ^i=biv−b−ln⁡((v−b)PRT)−2∑k=1mykaikRTv\ln \hat{\varphi}_{i}=\dfrac{b_{i}}{v-b}-\ln \left(\dfrac{(v-b) P}{R T}\right)-\dfrac{2 \sum\limits_{k=1}^{m} y_{k} a_{i k}}{R T v}
Description Redlich-Kwong EOS
Pure species i ln⁡φi=zi−1−ln⁡((vi−bi)PRT)−aibiRT1.5ln⁡(1+bivi)\begin{aligned}\ln \varphi_{i} =& z_{i}-1-\ln \left(\dfrac{\left(v_{i}-b_{i}\right) P}{R T}\right) \\ &- \dfrac{a_{i}}{b_{i} R T^{1.5}} \ln \left(1+\dfrac{b_{i}}{v_{i}}\right)\end{aligned}
Species 1 in a binary mixture ln⁡φ^1=b1b(z−1)−ln⁡((v−b)PRT)+1bRT1.5[ab1b−2(y1a1+y2a12)]ln⁡(1+bv)\begin{aligned}\ln \hat{\varphi}_{1} =& \dfrac{b_{1}}{b}(z-1)-\ln \left(\dfrac{(v-b) P}{R T}\right) \\ &+ \dfrac{1}{b R T^{1.5}}\left[\dfrac{a b_{1}}{b}-2\left(y_{1} a_{1}+y_{2} a_{12}\right)\right] \ln \left(1+\dfrac{b}{v}\right)\end{aligned}
Species i in a mixture ln⁡φ^i=bib(z−1)−ln⁡((v−b)PRT)+1bRT1.5[abib−2∑k=1mykaik]ln⁡(1+bv)\begin{aligned}\ln \hat{\varphi}_{i} =& \dfrac{b_{i}}{b}(z-1)-\ln \left(\dfrac{(v-b) P}{R T}\right) \\ &+ \dfrac{1}{b R T^{1.5}}\left[\dfrac{a b_{i}}{b}-2 \sum\limits_{k=1}^{m} y_{k} a_{i k}\right] \ln \left(1+\dfrac{b}{v}\right)\end{aligned}
Description Peng-Robinson EOS
Pure species i ln⁡φi=zi−1−ln⁡((vi−bi)PRT)−(aα)i22biRTln⁡[vi+(1+2)bivi+(1−2)bi]\ln \varphi_{i}= z_{i}-1-\ln \left(\dfrac{\left(v_{i}-b_{i}\right) P}{R T}\right)-\dfrac{(a \alpha)_{i}}{2 \sqrt{2} b_{i} R T} \ln \left[\dfrac{v_{i}+(1+\sqrt{2}) b_{i}}{v_{i}+(1-\sqrt{2}) b_{i}}\right]
Species 1 in a binary mixture ln⁡φ^1=b1b(z−1)−ln⁡((v−b)PRT)+aα22bRT[b1b−2aα(y1(aα)1+y2(aα)12)]ln⁡[v+(1+2)bv+(1−2)b]\begin{aligned}\ln \hat{\varphi}_{1} =& \dfrac{b_{1}}{b}(z-1)-\ln \left(\dfrac{(v-b) P}{R T}\right) \\ &+ \dfrac{a \alpha}{2 \sqrt{2} b R T}\left[\dfrac{b_{1}}{b}-\dfrac{2}{a \alpha}\left(y_{1}(a \alpha)_{1}+y_{2}(a \alpha)_{12}\right)\right] \ln \left[\dfrac{v+(1+\sqrt{2}) b}{v+(1-\sqrt{2}) b}\right]\end{aligned}
Species i in a mixture ln⁡φ^i=bib(z−1)−ln⁡((v−b)PRT)+aα22bRT[bib−2aα∑k=1myk(aα)ik]ln⁡[v+(1+2)bv+(1−2)b]\begin{aligned}\ln \hat{\varphi}_{i} =& \dfrac{b_{i}}{b}(z-1)-\ln \left(\dfrac{(v-b) P}{R T}\right) \\ &+ \dfrac{a \alpha}{2 \sqrt{2} b R T}\left[\dfrac{b_{i}}{b}-\dfrac{2}{a \alpha} \sum\limits_{k=1}^{m} y_{k}(a \alpha)_{i k}\right] \ln \left[\dfrac{v+(1+\sqrt{2}) b}{v+(1-\sqrt{2}) b}\right]\end{aligned}
Description Equations
Interaction parameter aa for multicomponent mixtures amix=∑∑yiyjaija_{\text{mix}} = \sum\sum y_i y_j a_{ij}
Like attractions aii=aia_{ii} = a_i
Unlike attractions aij=aiiajj(1−kij)a_{ij} = \sqrt{a_{ii}a_{jj}}(1 - k_{ij})
Volume parameter aa for multicomponent mixtures bmix=∑yibib_{\text{mix}} = \sum y_i b_{i}
Description Equations
Volume change of mixing Δvmix=0\Delta v_{\text{mix}} = 0
Enthalpy change of mixing Δhmix=0\Delta h_{\text{mix}} = 0
Entropy change of mixing Δsmix=−R∑yiln⁡yi>0\Delta s_{\text{mix}} = -R\sum y_i \ln y_i > 0
Gibbs energy change of mixing Δgmix=RT∑yiln⁡yi<0\Delta g_{\text{mix}} = RT \sum y_i \ln y_i < 0
Description Equations
Reference state of fugacity in ideal solution f^i∘=xifi∘\hat{f}_i^\circ = x_i f_i^\circ
Lewis/Randall rule reference state of fugacity
★ Solvent, pure limit
★ Same species (a-a) interaction only		 fi∘=fif^i∘=xifif_i^\circ = f_i \newline \hat{f}_i^\circ = x_i f_i
Henry’s law reference state of fugacity
★ Solute, dilute limit
★ Different species (a-b) interaction only		 fi∘=Hif^i∘=xiHif_i^\circ = \mathcal{H}_i \newline \hat{f}_i^\circ = x_i \mathcal{H}_i
Description Equations
Lewis/Randall rule reference state of fugacity
★ Solvent, pure limit
★ Same species (a-a) interaction only		 fi∘=fif^i∘=xifif_i^\circ = f_i \newline \hat{f}_i^\circ = x_i f_i
Pure liquid fugacity with Poynting correction at T, P fil=φisatPisatexp⁡[∫PisatPvilRTdP]f_i^l = \varphi_i^{\text{sat}} P_i^{\text{sat}} \exp\left[ \displaystyle\int_{P_i^{\text{sat}}}^{P} \dfrac{v_i^l}{RT} dP \right]
Pure liquid fugacity with Poynting correction at T, P
★ Incompressible liquid		 fil=φisatPisatexp⁡[vilRT(P−Pisat)]f_i^l = \varphi_i^{\text{sat}} P_i^{\text{sat}} \exp\left[ \dfrac{v_i^l}{RT} (P - P_i^{\text{sat}}) \right]
Pure liquid fugacity
★ P≈PsatP \approx P^{\text{sat}}		 fil=φisatPisatf_i^l = \varphi_i^{\text{sat}} P_i^{\text{sat}}
Pure liquid fugacity
★ Ideal gas (low P, low sat P)		 fil=Pisatf_i^l = P_i^{\text{sat}}
Description Equations
Henry’s law reference state of fugacity
★ Solute, dilute limit
★ Different species (a-b) interaction only		 fi∘=Hif^i∘=xiHif_i^\circ = \mathcal{H}_i \newline \hat{f}_i^\circ = x_i \mathcal{H}_i
Pressure dependence of Henry’s constant Hi(P)=Hi(P1)exp⁡[∫P0PV‾i∞RTdP]\mathcal{H}_i(P) = \mathcal{H}_i(P_1) \exp\left[ \displaystyle\int_{P_0}^{P} \dfrac{\overline{V}_i^\infty}{RT} dP \right]
Temperature dependence of Henry’s constant Hi(T)=Hi(T1)exp⁡[∫T0Thiv−H‾i∞RT2dP]\mathcal{H}_i(T) = \mathcal{H}_i(T_1) \exp\left[ \displaystyle\int_{T_0}^{T} \dfrac{h_i^v - \overline{H}_i^\infty}{RT^2} dP \right]
Description Equations
Activity coefficient γi=f^ilf^i∘=f^ilxifi∘\gamma_i = \dfrac{\hat{f}_i^l}{\hat{f}_i^\circ} = \dfrac{\hat{f}_i^l}{x_i f_i^\circ}
Activity coefficient in Lewis/Randall rule reference state lim⁡xi→0γiLR=Hifilim⁡xi→1γiLR=1\lim\limits_{x_i \to 0} \gamma_i^{\text{LR}} = \dfrac{\mathcal{H}_i}{f_i} \newline \lim\limits_{x_i \to 1} \gamma_i^{\text{LR}} = 1
Activity coefficient in Henry’s law reference state lim⁡xi→0γiH=1lim⁡xi→1γiH=fiHi\lim\limits_{x_i \to 0} \gamma_i^{\text{H}} = 1 \newline \lim\limits_{x_i \to 1} \gamma_i^{\text{H}} = \dfrac{f_i}{\mathcal{H}_i}
Activity ai=f^ilfi∘ai=xiγia_i = \dfrac{\hat{f}_i^l}{f_i^\circ} \newline a_i = x_i \gamma_i
Gibbs-Duhem Equation
★ Constant T, P		 ∑xid(ln⁡γi)=0\sum x_i d(\ln \gamma_i) = 0
Corollary of Gibbs-Duhem equation
★ Binary mixture		 x1(∂ln⁡γ1∂x1)T,P+x2(∂ln⁡γ2∂x2)T,P=0x_1 \left(\dfrac{\partial \ln \gamma_1}{\partial x_1}\right)_{T, P} + x_2 \left(\dfrac{\partial \ln \gamma_2}{\partial x_2}\right)_{T, P} = 0
Description Equations
Excess property kE=kreal−kidealk^E = k^{\text{real}} - k^{\text{ideal}}
Excess property kE=Δkmixreal−Δkmixidealk^E = \Delta k_{\text{mix}}^{\text{real}} - \Delta k_{\text{mix}}^{\text{ideal}}
Partial molar excess property K‾iE=K‾ireal−K‾iideal\overline{K}_i^E = \overline{K}_i^{\text{real}} - \overline{K}_i^{\text{ideal}}
Excess Gibbs free energy gE=Δgmix−RT∑xiln⁡xig^E = \Delta g_{\text{mix}} - RT \sum x_i \ln x_i
Excess Gibbs free energy gE=RT∑xiln⁡γig^E = RT \sum x_i \ln \gamma_i
Partial molar excess Gibbs free energy G‾iE=RTln⁡γi\overline{G}_i^E = RT \ln \gamma_i
Area test for thermodynamic consistency
★ Lewis/Randall reference state
★ Constant T, P		 ∫01ln⁡(γaγb)dxa=0\displaystyle\int_0^1 \ln \left(\dfrac{\gamma_a}{\gamma_b}\right) dx_a = 0
Description Equations
Two-suffix Margules equation gE=Axaxbg^E = A x_a x_b
Activity coefficient G‾iE=RTln⁡γiG‾aE=Axb2G‾bE=Axa2\overline{G}_i^{E} = RT\ln\gamma_i \newline \overline{G}_a^{E} = A x_b^2 \newline \overline{G}_b^{E} = A x_a^2
Description Equations
Three-suffix Margules equation gE=xaxb[A+B(xa−xb)]g^E = x_{a} x_{b}[A+B(x_{a}-x_{b})]
Activity coefficient G‾iE=RTln⁡γiG‾aE=(A+3B)xb2−4Bxb3G‾bE=(A−3B)xa2+4Bxa3\overline{G}_i^{E} = RT\ln\gamma_i \newline \overline{G}_a^{E} = (A+3 B) x_{b}^{2}-4 B x_{b}^{3} \newline \overline{G}_b^{E} = (A-3 B) x_{a}^{2}+4 B x_{a}^{3}
Three-suffix Margules equation gE=xaxb(Abaxa+Aabxb)g^E = x_{a} x_{b}(A_{ba} x_{a}+A_{ab} x_{b})
Activity coefficient G‾iE=RTln⁡γiG‾aE=xb2[Aab+2(Aba−Aab)xa]G‾bE=xa2[Aba+2(Aab−Aba)xb]\overline{G}_i^{E} = RT\ln\gamma_i \newline \overline{G}_a^{E} = x_{b}^{2}\left[A_{a b}+2\left(A_{b a}-A_{ab}\right) x_{a}\right] \newline \overline{G}_b^{E} = x_{a}^{2}\left[A_{b a}+2\left(A_{a b}-A_{b a}\right) x_{b}\right]
Description Equations
van Laar equation gE=xaxb(ABAxa+Bxb)g^E = x_{a} x_{b}\left(\dfrac{A B}{A x_{a}+B x_{b}}\right)
Activity coefficient G‾iE=RTln⁡γiG‾aE=A(BxbAxa+Bxb)2G‾bE=B(AxaAxa+Bxb)2\overline{G}_i^{E} = RT\ln\gamma_i \newline \overline{G}_a^{E} = A\left(\dfrac{B x_{b}}{A x_{a}+B x_{b}}\right)^{2} \newline \overline{G}_b^{E} = B\left(\dfrac{A x_{a}}{A x_{a}+B x_{b}}\right)^{2}
Description Equations
Wilson equation gE=−RT[xaln⁡(xa+Λabxb)+xbln⁡(xb+Λbaxa)]g^E = -R T\left[x_{a} \ln \left(x_{a}+\Lambda_{a b} x_{b}\right) + x_{b} \ln \left(x_{b}+\Lambda_{b a} x_{a}\right)\right]
Activity coefficient G‾iE=RTln⁡γiG‾aE=−RT[ln⁡(xa+Λabxb)+xb(Λbaxb+Λbaxa−Λabxa+Λabxb)]G‾bE=−RT[ln⁡(xb+Λbaxa)+xa(Λabxa+Λabxb−Λbaxb+Λbaxa)]\begin{aligned} \overline{G}_i^{E} &= RT\ln\gamma_i \\ \overline{G}_a^{E} &= -R T\left[\ln \left(x_{a}+\Lambda_{ab} x_{b}\right)+x_{b}\left(\dfrac{\Lambda_{b a}}{x_{b}+\Lambda_{ba}x_{a}}-\dfrac{\Lambda_{a b}}{x_{a}+\Lambda_{a b} x_{b}}\right)\right] \\ \overline{G}_b^{E} &= -R T\left[\ln \left(x_{b}+\Lambda_{ba}x_{a}\right)+x_{a}\left(\dfrac{\Lambda_{a b}}{x_{a}+\Lambda_{a b} x_{b}}-\dfrac{\Lambda_{b a}}{x_{b}+\Lambda_{ba}x_{a}}\right)\right] \end{aligned}
Wilson parameters Λab=vbvaexp⁡(−λabRT)Λba=vavbexp⁡(−λbaRT)\Lambda_{ab} = \dfrac{v_b}{v_a}\exp\left(-\dfrac{\lambda_{ab}}{RT}\right) \newline \Lambda_{ba} = \dfrac{v_a}{v_b}\exp\left(-\dfrac{\lambda_{ba}}{RT}\right)
Description Equations
Non-random two-liquid model (NRTL) gE=RTxaxb[τbaGbaxa+xbGba+τabGabxb+xaGab]g^E = R T x_{a} x_{b}\left[\dfrac{\tau_{b a} \mathbf{G}_{b a}}{x_{a}+x_{b} \mathbf{G}_{b a}}+\dfrac{\tau_{a b} \mathbf{G}_{a b}}{x_{b}+x_{a} \mathbf{G}_{a b}}\right]
Activity coefficient G‾iE=RTln⁡γiG‾aE=RTxb2[τbaGba2(xa+xbGba)2+τabGab(xb+xaGab)2]G‾bE=RTxa2[τbaGba(xa+xbGba)2+τabGab2(xa+xbGab)2]\overline{G}_i^{E} = RT\ln\gamma_i \newline \overline{G}_a^{E} = R T x_{b}^{2}\left[\dfrac{\tau_{b a} \mathbf{G}_{b a}^{2}}{\left(x_{a}+x_{b} \mathbf{G}_{b a}\right)^{2}}+\dfrac{\tau_{a b} \mathbf{G}_{a b}}{\left(x_{b}+x_{a} \mathbf{G}_{a b}\right)^{2}}\right] \newline \overline{G}_b^{E} = R T x_{a}^{2}\left[\dfrac{\tau_{b a} \mathbf{G}_{b a}}{\left(x_{a}+x_{b} \mathbf{G}_{b a}\right)^{2}}+\dfrac{\tau_{a b} \mathbf{G}_{a b}^{2}}{\left(x_{a}+x_{b} \mathbf{G}_{a b}\right)^{2}}\right]
NRTL parameters Gab=exp⁡(−ατab)Gba=exp⁡(−ατba)\mathbf{G}_{ab} = \exp(-\alpha \tau_{ab}) \newline \mathbf{G}_{ba} = \exp(-\alpha \tau_{ba})
Description Equations
Two-suffix Margules equation (ternary system) gE=Aabxaxb+Aacxaxc+Abcxbxcg^E = A_{ab}x_a x_b + A_{ac}x_a x_c + A_{bc}x_b x_c
Partial excess Gibbs energy of species a G‾aE=Aabxb2+Aacxc2+(Aab+Aac−Abc)xbxc\overline{G}^E_a = A_{ab}x_b^2 + A_{ac}x_c^2 + (A_{ab} + A_{ac} - A_{bc})x_b x_c
Partial excess Gibbs energy of species b G‾bE=Aabxa2+Abcxc2+(Aab+Abc−Aac)xaxc\overline{G}^E_b = A_{ab}x_a^2 + A_{bc}x_c^2 + (A_{ab} + A_{bc} - A_{ac})x_a x_c
Partial excess Gibbs energy of species c G‾cE=Aacxa2+Abcxb2+(Aac+Abc−Aab)xaxb\overline{G}^E_c = A_{ac}x_a^2 + A_{bc}x_b^2 + (A_{ac} + A_{bc} - A_{ab})x_a x_b
Two-suffix Margules equation (multicomponent system) gE=∑i∑jAij2xixjg^E = \sum\limits_i \sum\limits_j \dfrac{A_{ij}}{2}x_i x_j
Two-suffix Margules parameter Aii=0Aij=AjiA_{ii} = 0 \newline A_{ij} = A_{ji}
Description Equations
Wilson equation ln⁡γi=1−ln⁡(∑j=1mxjΛij)−∑k=1mxkΛkiln⁡(∑j=1mxjΛkj)\begin{aligned}\ln \gamma_i = 1-\ln \left(\sum\limits_{j=1}^{m} x_{j} \Lambda_{i j}\right)-\sum\limits_{k=1}^{m} \dfrac{x_{k} \Lambda_{k i}}{\ln \left(\sum\limits_{j=1}^{m} x_{j} \Lambda_{k j}\right)}\end{aligned}
Wilson parameter Λjj=1\Lambda_{jj} = 1
Description Equations
Non-random two-liquid model (NRTL) ln⁡γi=∑j=1mτjixjGji∑l=1mxlGli+∑j=1mxjGij∑l=1mxlGlj(τij−∑k=1mτkjxkGkj∑l=1mxlGlj)\begin{aligned}\ln \gamma_i = \frac{\sum\limits_{j=1}^{m} \tau_{j i} x_{j} \mathbf{G}_{j i}}{\sum\limits_{l=1}^{m} x_{l} \mathbf{G}_{l i}}+\sum\limits_{j=1}^{m} \frac{x_{j} \mathbf{G}_{i j}}{\sum\limits_{l=1}^{m} x_{l} \mathbf{G}_{l j}}\left(\tau_{i j}-\frac{\sum\limits_{k=1}^{m} \tau_{k j} x_{k} \mathbf{G}_{k j}}{\sum\limits_{l=1}^{m} x_{l} \mathbf{G}_{l j}}\right) \end{aligned}
NRTL parameters ln⁡Gij=−αijτijτij=0Gij=1\ln \mathbf{G}_{i j}=-\alpha_{i j} \tau_{i j} \newline \tau_{i j}=0 \newline \mathbf{G}_{i j}=1
Description Equations
Universal quasi-chemical theory (UNIQUAC) ln⁡γi=ln⁡Φi∗xi+z2qiln⁡θiΦi∗+li+Φi∗xi∑j=1mxjlj+qi′[1−∑j=1mθj′τji−∑j=1mθj′τij∑k=1mθk′τkj]\begin{aligned} \ln\gamma_i = \ln \frac{\Phi_{i}^{*}}{x_{i}}+\frac{z}{2} q_{i} \ln \frac{\theta_{i}}{\Phi_{i}^{*}}+l_{i}+\frac{\Phi_{i}^{*}}{x_{i}} \sum\limits_{j=1}^{m} x_{j} l_{j}+q_{i}^{\prime}\left[1-\sum\limits_{j=1}^{m} \theta_{j}^{\prime} \tau_{j i}-\sum\limits_{j=1}^{m} \frac{\theta_{j}^{\prime} \tau_{i j}}{\sum\limits_{k=1}^{m} \theta_{k}^{\prime} \tau_{k j}}\right] \end{aligned}
UNIQUAC parameters li=z2(ri−qi)−(ri−1)τjk=exp⁡(−ajkT)τkk=1Φi∗=xiri∑j=1mxjrjθi=xiqi∑j=1mxjqjθi′=xiqi′∑j=1mxjqj′l_{i}=\dfrac{z}{2}\left(r_{i}-q_{i}\right)-\left(r_{i}-1\right) \newline \tau_{j k}=\exp \left(-\dfrac{a_{j k}}{T}\right) \newline \tau_{k k}=1 \newline \Phi_{i}^{*}=\dfrac{x_{i} r_{i}}{\sum\limits_{j=1}^{m} x_{j} r_{j}} \newline \theta_{i}=\dfrac{x_{i} q_{i}}{\sum\limits_{j=1}^{m} x_{j} q_{j}} \newline \theta_{i}^{\prime}=\dfrac{x_{i} q_{i}^{\prime}}{\sum\limits_{j=1}^{m} x_{j} q_{j}^{\prime}}
Description Equations
Excess Gibbs energy dependence on pressure (∂gE∂P)T,ni=vE=Δvmix\left(\dfrac{\partial g^E}{\partial P}\right)_{T, n_i} = v^E = \Delta v_{\text{mix}}
Excess Gibbs energy dependence on temperature [∂∂T(gET)]P,ni=−hET2=−ΔhmixT2\left[\dfrac{\partial}{\partial T}\left(\dfrac{g^E}{T}\right)\right]_{P, n_i} = -\dfrac{h^E}{T^2} = -\dfrac{\Delta h_{\text{mix}}}{T^2}
Excess Gibbs energy dependence on temperature
★ Regular solution		 gE=RT∑xiln⁡γi=constantg^E = RT\sum x_i \ln \gamma_i = \text{constant}
Excess Gibbs energy dependence on temperature
★ Athermal solution		 gET=R∑xiln⁡γi=constant\dfrac{g^E}{T} = R\sum x_i \ln \gamma_i = \text{constant}
Description Equations
Activity coefficient dependence on pressure (∂ln⁡γi∂P)T,x=V‾i−viRT\left(\dfrac{\partial \ln\gamma_i}{\partial P}\right)_{T, x} = \dfrac{\overline{V}_i - v_i}{RT}
Activity coefficient dependence on temperature (∂ln⁡γi∂T)P,x=−H‾i−hiRT2\left(\dfrac{\partial \ln\gamma_i}{\partial T}\right)_{P, x} = -\dfrac{\overline{H}_i - h_i}{RT^2}
Description Equations
Activity coefficient of pure solids Γi=1\Gamma_i = 1
Fugacity of pure solids f^is=fis\hat{f}_i^s = f_i^s
Fugacity of solid solutions
★ Treat like liquid solution		 f^is=XiΓifis\hat{f}_i^s = X_i \Gamma_i f_i^s
Description Equations
General VLE condition f^iv=f^ilyiφ^ivP=xiγilfi∘\begin{aligned} \hat{f}_i^v &= \hat{f}_i^l \\ y_i \hat{\varphi}_i^v P &= x_i \gamma_i^l f_i^\circ \end{aligned}
Description Equations
Raoult’s law
★ Ideal gas φ^iv=1\hat{\varphi}_i^v = 1
★ Ideal solution γil=1\gamma_i^l = 1
★ Lewis/Randall ref state fi∘=fi=Pisatf_i^\circ = f_i = P_i^{\text{sat}}		 yiP=xiPisaty_i P = x_i P_i^{\text{sat}}
KK-value Ki=PisatPK_i = \dfrac{P_i^{\text{sat}}}{P}
Partial pressure relation of binary system P=yaP+ybP=xaPasat+(1−xa)Pbsat\begin{aligned}P &= y_a P + y_b P \\ &= x_a P_a^{\text{sat}} + (1-x_a)P_b^{\text{sat}}\end{aligned}
Vapor phase composition of binary system ya=xaPasatxaPasat+(1−xa)Pbsaty_a = \dfrac{x_a P_a^{\text{sat}}}{x_a P_a^{\text{sat}} + (1-x_a)P_b^{\text{sat}}}
Partial pressure relation of multicomponent system P=∑yiP=∑xiPisat\begin{aligned}P &= \textstyle\sum y_i P \\ &= \textstyle\sum x_i P_i^{\text{sat}}\end{aligned}
Vapor phase composition of multicomponent system yi=xiPisat∑xiPisaty_i = \dfrac{x_i P_i^{\text{sat}}}{\sum x_i P_i^{\text{sat}}}
Description Equations
Nonideal liquid solution
★ Ideal gas φ^iv=1\hat{\varphi}_i^v = 1
★ Lewis/Randall ref state fi∘=fi=Pisatf_i^\circ = f_i = P_i^{\text{sat}}		 yiP=xiγiPisaty_i P = x_i \gamma_i P_i^{\text{sat}}
Partial pressure relation of binary system P=yaP+ybP=xaγaPasat+(1−xa)γbPbsat\begin{aligned}P &= y_a P + y_b P \\ &= x_a \gamma_a P_a^{\text{sat}} + (1-x_a) \gamma_b P_b^{\text{sat}}\end{aligned}
Vapor phase composition of binary system ya=xaγaPasatxaγaPasat+(1−xa)γbPbsaty_a = \dfrac{x_a \gamma_a P_a^{\text{sat}}}{x_a \gamma_a P_a^{\text{sat}} + (1-x_a) \gamma_b P_b^{\text{sat}}}
Partial pressure relation of multicomponent system P=∑yiP=∑xiγiPisat\begin{aligned}P &= \textstyle\sum y_i P \\ &= \textstyle\sum x_i \gamma_i P_i^{\text{sat}}\end{aligned}
Vapor phase composition of multicomponent system yi=xiγiPisat∑xiγiPisaty_i = \dfrac{x_i \gamma_i P_i^{\text{sat}}}{\sum x_i \gamma_i P_i^{\text{sat}}}
Description Equations
Azeotrope xi=yix_i = y_i
Azeotrope equilibrium consition P=γiPisatP = \gamma_i P_i^{\text{sat}}
Activity coefficient from azeotrope γi=PPisat\gamma_i = \dfrac{P}{P_i^{\text{sat}}}
Activity coefficient ratio from azeotrope γaγb=PbsatPasat\dfrac{\gamma_a}{\gamma_b} = \dfrac{P_b^{\text{sat}}}{P_a^{\text{sat}}}
Description Equations
Least square objective function based on pressure fP=∑(P−Pcalc)i2f_P = \sum (P - P_{\text{calc}})_i^2
Least square objective function based on excess Gibbs energy fgE=∑(gE−gcalcE)i2f_{g^E} = \sum (g^E - g^E_{\text{calc}})_i^2
Least square objective function based on activity coefficient for binary system fγ=∑[(γa−γacalcγa)2−(γb−γbcalcγb)2]if_\gamma = \sum \left[ \left(\dfrac{\gamma_a - \gamma_a^{\text{calc}}}{\gamma_a}\right)^2 - \left(\dfrac{\gamma_b - \gamma_b^{\text{calc}}}{\gamma_b}\right)^2 \right]_i
Ideal gas Nonideal gas
Ideal liquid Solute a yaP=xaHay_a P = x_a \mathcal{H}_a yaφaP=xaHaexp⁡[∫P0PV‾a∞RTdP]y_a \varphi_a P = x_a \mathcal{H}_a \exp\left[\displaystyle\int_{P_0}^P \dfrac{\overline{V}_a^\infty}{RT} dP\right]
Solvent b ybP=xbPbsaty_b P = x_b P_b^{\text{sat}} ybφ^bP=xbφbsatPbsatexp⁡[∫PbsatPvblRTdP]y_b \hat{\varphi}_b P = x_b \varphi_b^{\text{sat}} P_b^{\text{sat}} \exp\left[\displaystyle\int_{P_b^{\text{sat}}}^P \dfrac{v_b^l}{RT} dP\right]
Nonideal liquid Solute a yaP=xaγaHHay_a P = x_a \gamma_a^\mathrm{H} \mathcal{H}_a yaφaP=xaγaHHaexp⁡[∫P0PV‾a∞RTdP]y_a \varphi_a P = x_a \gamma_a^{\mathrm{H}} \mathcal{H}_a \exp\left[\displaystyle\int_{P_0}^P \dfrac{\overline{V}_a^\infty}{RT} dP\right]
Solvent b ybP=xbγbPbsat\begin{aligned} y_b P = x_b \gamma_b P_b^{\text{sat}} \end{aligned} ybφ^bP=xbγbφbsatPbsatexp⁡[∫PbsatPvblRTdP]\begin{aligned} y_b \hat{\varphi}_b P = x_b \gamma_b \varphi_b^{\text{sat}} P_b^{\text{sat}} \exp\left[\displaystyle\int_{P_b^{\text{sat}}}^P \dfrac{v_b^l}{RT} dP\right] \end{aligned}
Description Equations
Mixing rule for Henry’s constant ln⁡Ha=∑jxiln⁡Ha,j\ln\mathcal{H}_a = \sum\limits_j x_i \ln\mathcal{H}_{a, j}
Description Equations
General LLE condition f^iα=f^iβxiαγiα=xiβγiβ\begin{aligned}\hat{f}_i^\alpha &= \hat{f}_i^\beta \\ x_i^\alpha \gamma_i^\alpha &= x_i^\beta \gamma_i^\beta \end{aligned}
Compositions xaα,xbα,xaβ,xbβx_a^\alpha, x_b^\alpha, x_a^\beta, x_b^\beta
★ Two-suffix Margules equation		 xaαexp⁡[ART(xbα)2]=xaβexp⁡[ART(xbβ)2]xbαexp⁡[ART(xaα)2]=xbβexp⁡[ART(xaβ)2]xaα+xbα=1xaβ+xbβ=1\begin{aligned} x_a^{\alpha}\exp \left[\dfrac{A}{RT}\left(x_b^{\alpha}\right)^2\right] &= x_a^{\beta}\exp \left[\dfrac{A}{RT}\left(x_b^{\beta}\right)^2\right] \\ x_b^{\alpha}\exp \left[\dfrac{A}{RT}\left(x_a^{\alpha}\right)^2\right] &= x_b^{\beta}\exp \left[\dfrac{A}{RT}\left(x_a^{\beta}\right)^2\right] \\ x_a^\alpha + x_b^\alpha &= 1 \\ x_a^\beta + x_b^\beta &= 1 \end{aligned}
Genral criteria for instability (separation) (∂g2∂xa2)T,P<0\left(\dfrac{\partial g^2}{\partial x_a^2}\right)_{T,P} < 0
Criteria for instability (separation)
★ Two-suffix Margules equation		 RTxaxb<2A\dfrac{RT}{x_ax_b} < 2A
Upper consolute temperature
★ Two-suffix Margules equation		 Tu=A2RT_u = \dfrac{A}{2R}
Description Equations
General VLLE condition f^iv=f^iα=f^iβ\hat{f}_i^v = \hat{f}_i^\alpha = \hat{f}_i^\beta
Composition and state variables xaα,xbα,xaβ,xbβ,ya,yb,T,Px_a^\alpha, x_b^\alpha, x_a^\beta, x_b^\beta, y_a, y_b, T, P
★ Two-suffix Margules equation		 yaP=xaαexp⁡[ART(xbα)2]Pasat=xaβexp⁡[ART(xbβ)2]PasatybP=xbαexp⁡[ART(xaα)2]Pbsat=xbβexp⁡[ART(xaβ)2]Pbsatya+yb=1xaα+xbα=1xaβ+xbβ=1\begin{aligned} y_aP = x_a^{\alpha }\exp \left[\frac{A}{RT}\left(x_b^{\alpha }\right)^2\right]P_a^{\text{sat}} &= x_a^{\beta }\exp \left[\frac{A}{RT}\left(x_b^{\beta }\right)^2\right]P_a^{\text{sat}} \\ y_b P = x_b^{\alpha }\exp \left[\frac{A}{RT}\left(x_a^{\alpha }\right)^2\right]P_b^{\text{sat}} &= x_b^{\beta }\exp \left[\frac{A}{RT}\left(x_a^{\beta }\right)^2\right]P_b^{\text{sat}} \\ y_a + y_b &= 1 \\ x_a^\alpha + x_b^\alpha &= 1 \\ x_a^\beta + x_b^\beta &= 1 \end{aligned}
Description Equations
General SLE condition f^is=f^ilXiΓifis=xiγifilfs=xiγifil\begin{aligned}\hat{f}_i^s &= \hat{f}_i^l \\ X_i \Gamma_i f_i^s &= x_i \gamma_i f_i^l \\ f_s &= x_i \gamma_i f_i^l \end{aligned}
Composition of SLE
★ Pure solid		 ln⁡[xiγi]=Δhfus,TmR[1T−1Tm]−1R∫TmTΔcPslTdT+1RT∫TmTΔcPsldT\displaystyle\ln \left[x_i\gamma_i\right]=\frac{\Delta h_{\text{fus},T_m}}{R}\left[\frac{1}{T}-\frac{1}{T_m}\right]-\frac{1}{R}\int_{T_m}^T\frac{\Delta c_P^{sl}}{T}dT+\frac{1}{RT}\int _{T_m}^T\Delta c_P^{sl}dT
Composition of SLE
★ Pure solid.
★ Constant ΔcPsl\Delta c_P^{sl}		 ln⁡[xiγi]=Δhfus,TmR[1T−1Tm]−ΔcPslR[1−TmT−ln⁡(TTm)]\displaystyle\ln \left[x_i\gamma_i\right]=\frac{\Delta h_{\text{fus},T_m}}{R}\left[\frac{1}{T}-\frac{1}{T_m}\right]-\frac{\Delta c_P^{sl}}{R}\left[1-\frac{T_m}{T}-\ln \left(\frac{T}{T_m}\right)\right]
Composition of SLE
★ Solid solution		 ln⁡[xiγiXiΓi]=Δhfus,TmR[1T−1Tm]−1R∫TmTΔcPslTdT+1RT∫TmTΔcPsldT\begin{aligned}\displaystyle\ln \left[\dfrac{x_i\gamma_i}{X_i \Gamma_i}\right]=\frac{\Delta h_{\text{fus},T_m}}{R}\left[\frac{1}{T}-\frac{1}{T_m}\right]-\frac{1}{R}\int_{T_m}^T\frac{\Delta c_P^{sl}}{T}dT+\frac{1}{RT}\int _{T_m}^T\Delta c_P^{sl}dT\end{aligned}
Composition of SLE
★ Solid solution.
★ Constant ΔcPsl\Delta c_P^{sl}		 ln⁡[xiγiXiΓi]=Δhfus,TmR[1T−1Tm]−ΔcPslR[1−TmT−ln⁡(TTm)]\displaystyle\ln \left[\dfrac{x_i\gamma_i}{X_i \Gamma_i}\right]=\frac{\Delta h_{\text{fus},T_m}}{R}\left[\frac{1}{T}-\frac{1}{T_m}\right]-\frac{\Delta c_P^{sl}}{R}\left[1-\frac{T_m}{T}-\ln \left(\frac{T}{T_m}\right)\right]
Description Equations
Boiling point elevation
★ Solvent aa, solute bb		 T−Tboil=RTboil2ΔhvapγaxbT-T_{\text{boil}}=\dfrac{RT_{\text{boil}}^2}{\Delta h_{\text{vap}}} \gamma_a x_b
Activity coefficient from boiling point elevation data γb=(T−Tboil)ΔhvapRTboil2xb\gamma_b=\dfrac{\left(T-T_{\text{boil}}\right)\Delta h_{\text{vap}}}{RT_{\text{boil}}^2x_b}
Freezing point depression
★ Solvent aa, solute bb		 T−Tm=RTm2ΔhfusγaxbT-T_m=\dfrac{RT_m^2}{\Delta h_{\text{fus}}}\gamma_a x_b
Activity coefficient from freezing point depression data γb=(T−Tm)ΔhfusRTm2xb\gamma_b=\dfrac{\left(T-T_m\right)\Delta h_{\text{fus}}}{RT_m^2x_b}
Osmotic pressure Π=−RTvaln⁡(xaγa)\Pi =-\dfrac{RT}{v_a}\ln \left(x_a\gamma _a\right)
Osmotic pressure
★ Ideal solution, dilute bb		 Π=−RTvaxb\Pi =-\dfrac{RT}{v_a}x_b
Molar mass from osmotic pressure data Mb=RTCbΠ\mathcal{M}_b = \dfrac{RTC_b}{\Pi}
Description Equations
Chemical reaction expressed in stoichiometric coefficients ∑νiAi\sum \nu_i A_i
Extent of reaction dξ=dniνid\xi = \dfrac{dn_i}{\nu_i}
Moles of species ni=ni∘+νiξn_i = n_i^\circ + \nu_i \xi
Chemical equilibrium condition dGdξ=0=∑μiνi\dfrac{dG}{d\xi} = 0 = \sum \mu_i \nu_i
Gibbs energy of reaction Δgrxn∘=∑νigi∘\Delta g_{\text{rxn}}^\circ = \sum \nu_i g_i^\circ
Equilibrium constant K=∏(f^ifi∘)νiK = \prod \left(\dfrac{\hat{f}_i}{f_i^\circ}\right)^{\nu_i}
Equilibrium constant and Gibbs energy of reaction ln⁡K=−Δgrxn∘RT\ln K = -\dfrac{\Delta g_{\text{rxn}}^\circ}{RT}
Description Equations
Gibbs energy of formation method Δgrxn∘=∑νiΔgf,i∘\Delta g_{\text{rxn}}^\circ = \sum \nu_i \Delta g_{f, i}^\circ
TT dependence of KK ddTln⁡K=Δhrxn∘RT2\dfrac{d}{dT} \ln K = \dfrac{\Delta h_{\text{rxn}}^\circ}{RT^2}
TT dependence of KK
★ Constant Δhrxn∘\Delta h_{\text{rxn}}^\circ		 ln⁡(K1K2)=−Δhrxn∘R(1T2−1T1)\ln \left(\dfrac{K_1}{K_2}\right)=-\dfrac{\Delta h_{\text{rxn}}^{\circ }}{R}\left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)
TT dependence of KK
★ Δhrxn∘(T)\Delta h_{\text{rxn}}^\circ(T)		 ln⁡(K1K2)=−Δhrxn∘R(1T2−1T1)+∫T1T2∫T1T∑νicP,idTRT2dT\ln \left(\dfrac{K_1}{K_2}\right)=-\dfrac{\Delta h_{\text{rxn}}^{\circ }}{R}\left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right) + \displaystyle\int_{T_1}^{T_2}\dfrac{\int_{T_1}^T\sum\nu_i c_{P,i}dT}{RT^2}dT
Description Equations
General expression K=∏(yiφ^iPfi∘)νiK = \prod \left(\dfrac{y_i \hat{\varphi}_i P}{f_i^\circ}\right)^{\nu_i}
Lewis fugacity rule K=Pν∏(yiφi)νiK = P^\nu \prod \left(y_i \varphi_i\right)^{\nu_i}
Ideal gas K=Pν∏(yi)νiK = P^\nu \prod \left(y_i\right)^{\nu_i}
Description Equations
General expression K=∏(xiγififi∘)νiK = \prod \left(\dfrac{x_i \gamma_i f_i}{f_i^\circ}\right)^{\nu_i}
Low pressure, neglegible pressure dependence K=Pν∏(xiγi)νiK = P^\nu \prod \left(x_i \gamma_i\right)^{\nu_i}
Ideal solution K=Pν∏(xi)νiK = P^\nu \prod \left(x_i\right)^{\nu_i}
Description Equations
General expression K=∏(XiΓififi∘)νiK = \prod \left(\dfrac{X_i \Gamma_i f_i}{f_i^\circ}\right)^{\nu_i}
Low pressure, neglegible pressure dependence K=Pν∏(XiΓi)νiK = P^\nu \prod \left(X_i \Gamma_i\right)^{\nu_i}
Ideal solid solution K=Pν∏(Xi)νiK = P^\nu \prod \left(X_i\right)^{\nu_i}
Description Equations
Chemical reactions expressed in stoichiometric coefficients ∑k=1R∑i=1mνk,iAi\sum\limits_{k=1}^R\sum\limits_{i=1}^m\nu _{k,i}A_i
Moles of species ni=ni∘+∑k=1Rνk,iξn_i = n_i^\circ + \sum_{k=1}^R \nu_{k, i} \xi
Description Equations
Gibbs energy and non-Pv work δW∗≥(dG)T,P\delta W^* \ge (dG)_{T, P}
Gibbs energy of reaction and reversible work W=ΔG=zξFEW = \Delta G = z\xi FE
Nerst equation E=Erxn∘−RTzFln⁡[∏vap(Pi)νi∏liq(biγi)νi]E=E_{\text{rxn}}^{\circ }-\dfrac{RT}{zF}\ln \left[\prod\limits_{\text{vap}}(P_i)^{\nu_i} \prod\limits_{\text{liq}}(b_i \gamma_i)^{\nu_i}\right]
Standard Gibbs energy of reaction Δgrxn∘=−zFErxn∘\Delta g_{\text{rxn}}^{\circ }=-zFE_{\text{rxn}}^{\circ}
Standard potential of reaction Erxn∘=−Δgrxn∘zFE_{\text{rxn}}^{\circ}=-\dfrac{\Delta g_{\text{rxn}}^{\circ }}{zF}
Standard potential of reaction Erxn∘=Ered∘(cathode)−Ered∘(anode)E_{\text{rxn}}^{\circ} = E_{\text{red}}^{\circ}(\text{cathode}) - E_{\text{red}}^{\circ}(\text{anode})
Average activity coefficient XXa YXb⇌a XX(z+)++b YX(z−)−γ±=(γ+aγ−b)1/(a+b)\ce{X_a Y_b <=> aX^{(z_+) +} + bY^{(z_-) -}} \newline \gamma_\pm = (\gamma_+^a \gamma_-^b)^{1/(a+b)}
Average activity coefficient XY⇌XX++YX−γ±=γ+γ−\ce{XY <=> X+ + Y-} \newline \gamma_\pm = \sqrt{\gamma_+ \gamma_-}
Debye-Huckel model ln⁡γ±=−A∣z+z−∣I\ln \gamma_\pm = -A \vert z_+ z_- \vert \sqrt{I}
Ionic strength I=12∑zi2biI = \frac{1}{2}\sum z_i^2 b_i
Updated on 2022-03-15
Back | Home